题目内容
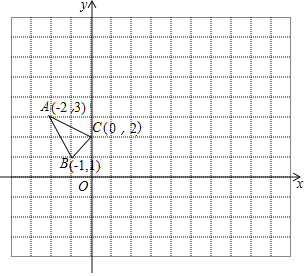
【题目】△ABC在平面直角坐标系xOy中的位置如图所示:
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点B1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点A2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点B走过的路径长为 ;
(4)在x轴上找一点P,使PB+PC的值最小,则点P的坐标为 .
【答案】(1)(1,﹣1);(2)(2,3);(3)![]() π;(4)(﹣
π;(4)(﹣![]() ,0).
,0).
【解析】
(1)利用关于原点对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可;
(2)利用关于平移变换的点的坐标特征写出A2、B2、C2的坐标,然后描点即可;
(3)利用弧长公式计算;
(4)连接BC1交x轴于P点,如图,利用两点之间线段最短得到此时PB+PC的值最小,利用待定系数法求出直线BC1的解析式为y=﹣3x﹣2,然后计算函数值为0对应的自变量的值即可得到P点坐标.
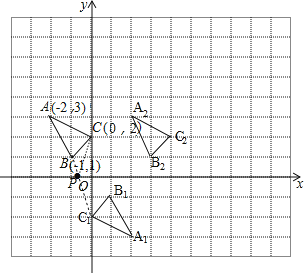
(1)如图,△A1B1C1为所作,点B1的坐标为(1,﹣1);
(2)如图,△A2B2C2为所作,点A2的坐标为(2,3);
(3)OB=![]() =
=![]() ,
,
点B走过的路径长=![]() =
=![]() π;
π;
(4)连接BC1交x轴于P点,如图,
则PC=PC1,
∴PB+PC=PB+PC1=BC1,
∴此时PB+PC的值最小,
设直线BC1的解析式为y=kx,
把B(﹣1,1),(0,﹣2)代入得﹣k+b=1,b=﹣2,
∴k=3,b=﹣2,
∴直线BC1的解析式为y=﹣3x﹣2,
当y=0时,﹣3x﹣2=0,解得x=![]() ,
,
∴点P的坐标为(﹣![]() ,0).
,0).

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的对应值如图,下列说法错误的是:( )
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是(0,4)
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而增大
【题目】某网店经市场调查,发现进价为40元的某新型文具每月的销售量y(件)与售价x(元)的相关信息如下:
售价x(元) | 60 | 70 | 80 | 90 | … |
销售量y(件) | 280 | 260 | 240 | 220 | … |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 (填“一次函数”、“反比例函数”或“二次函数”),并求这个函数关系式;
(2)当售价为多少元时,当月的销售利润最大,最大利润是多少;
(3)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大,最大利润是多少?