题目内容
【题目】在平面直角坐标系中,已知点A![]() ,点B
,点B![]() ,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
【答案】(0,![]() ),(0,
),(0,![]() )
)
【解析】
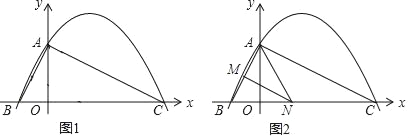
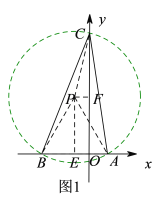
(1)如图1,以AB为边在x轴的上方作等边△PAB,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时∠BCA=30°,再根据题中的已知条件求得线段OC的长,即可得到此时点C的坐标;
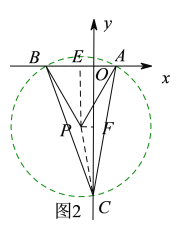
(2)如图2,和(1)同理在y轴的负半轴可求得另一个符合要求的点C的坐标.
(1)如图1,以AB为边在x轴的上方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,
∵点A、B的坐标分别为:![]() ,
,![]() ,
,
∴AB=![]() ,OB=
,OB=![]()
∴PA=PC=AB=![]() ,
,
过点P作PF⊥y轴于点F,PE⊥x轴于点E,则四边形PEOF是矩形,
∴OF=PE,PF=OE,
∵在等边△PAB中,PE=PA·sin60°=![]() ,BE=
,BE=![]() AB=
AB=![]() ,
,
∴OF=12,OE=OB-BE=![]() ,
,
∴PF=![]() ,
,
又∵在Rt△PFC中,PC=![]() ,∠PFC=90°,
,∠PFC=90°,
∴CF=![]() ,
,
∴OC=OF+CF=![]() ,
,
∴此时点C的坐标为![]() ;
;
(2)如图2,以AB为边在x轴的下方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的负半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,和(1)同理可得此时点C的坐标为:![]() ;
;
综上所述,符合条件的点![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目