Question

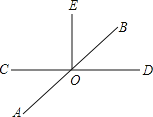
【题目】已知：如图，直线AB、CD相交于点O，EO⊥CD于O．

（1）若∠AOC=36°，求∠BOE的度数；

（2）若∠BOD：∠BOC=1：5，求∠AOE的度数；

（3）在（2）的条件下，请你过点O画直线MN⊥AB，并在直线MN上取一点F（点F与O不重合），然后直接写出∠EOF的度数．

Answer 1

【答案】（1）54°；（2）120°；（3）∠EOF的度数为30°或150°．

【解析】

（1）依据垂线的定义以及对顶角相等，即可得∠BOE的度数；

（2）依据平角的定义以及垂线的定义，即可得到∠AOE的度数；

（3）分两种情况：若F在射线OM上，则∠EOF=∠BOD=30°；若F'在射线ON上，则∠EOF'=∠DOE+∠BON-∠BOD=150°．

解：（1）∵EO⊥CD，

∴∠DOE=90°，

又∵∠BOD=∠AOC=36°，

∴∠BOE=90°-36°=54°；

（2）∵∠BOD：∠BOC=1：5，

∴∠BOD=∠COD=30°，

∴∠AOC=30°，

又∵EO⊥CD，

∴∠COE=90°，

∴∠AOE=90°+30°=120°；

（3）分两种情况：

若F在射线OM上，则∠EOF=∠BOD=30°；

若F'在射线ON上，则∠EOF'=∠DOE+∠BON-∠BOD=150°；

综上所述，∠EOF的度数为30°或150°．

故答案为：（1）54°；（2）120°；（3）∠EOF的度数为30°或150°．