��Ŀ����
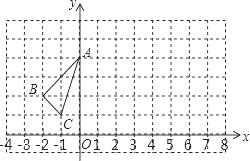
����Ŀ����ͼ��ʾ,������OABC����ƽ��ֱ������ϵ��,��A,C�ֱ���x,y�����������,��֪��B(4,2),������OABC����,ʹ�õ�C�Ķ�Ӧ��Pǡ�������߶�OA(�����˵�O,A)��,�ۺ�����ֱ�߷ֱ�BC��OA�ڵ�D��E������P���߶�OA���˶�ʱ,����P��OA�Ĵ��߽��ۺ�����ֱ���ڵ�Q.
��1����֤��CQ=QP
��2�����Q������Ϊ(x,y),��y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ;
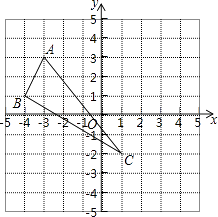
��3����ͼ2,����OQ,OB,����P���߶�OA���˶�ʱ,��������OBQ�����ΪS,��xȡ��ֵʱ,Sȡ����Сֵ,�������Сֵ��
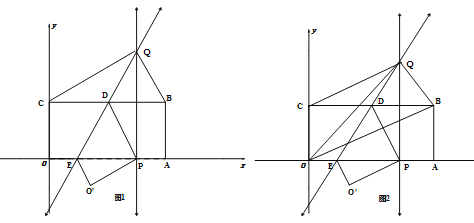
���𰸡���1��CQ=PQ��2��![]() ��3��
��3��![]()
�������������������1����CD=PD,��CDE=��PDE�õ���CDQ=��PDQ���ټ���DQ=DQ�ɵá�CDQ�ա�PDQ�����Ե�CQ=PQ����2����Q(x,y) ����CQ=PQ=y����QP��BC��H,��QH=y-2,CH=x���ɹ��ɶ�������![]() ������
������![]() ����3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)����
����3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)����![]() ������
������![]() ������
������![]() ������x=1ʱ��S����СֵΪ
������x=1ʱ��S����СֵΪ![]() ��
��
���������
��1������֪��CD=PD,��CDE=��PDE
�� ��CDQ=��PDQ
�֡�DQ=DQ
���CDQ�ա�PDQ
��CQ=PQ
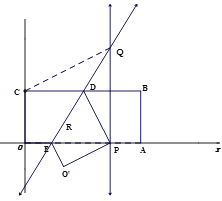
��2����Q(x,y)
CQ=PQ=y
��QP��BC��H,��QH=y-2,CH=x���ɹ��ɶ�������


��3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)������![]()
![]() .
.
![]()
![]()

����Ŀ��Ŀǰ���ҹ���Լ��1.3�ڸ�Ѫѹ�����ߣ�ռ15���������˿�����10%��15%��Ԥ����Ѫѹ���ݺ��ӡ���ǧ��kpa���͡�������mmHg�����DZ�ʾѪѹ�ĵ�λ��ǰ���Ƿ����Ĺ��ʼ�����λ�����������ǹ�ȥһֱ�㷺ʹ�õĹ��õ�λ����������±����ṩ����Ϣ���ж����и��黻������ȷ���ǣ� ��
ǧ��kpa | 10 | 12 | 16 | �� |
������mmHg | 75 | 90 | 120 | �� |
A. 18kpa=135mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 32kpa=240mmHg