ЬтФПФкШн
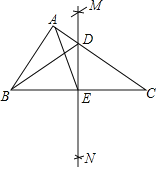
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊCЃЈ1ЃЌЉ2ЃЉЃЌжБЯпy=kx+mЕФЭМЯѓгыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌЦфжаAЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЌBЕудкyжсЩЯЃЎЕуPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЈЕуPгыЕуAЁЂBВЛжиКЯЃЉЃЌЙ§ЕуPЧвДЙжБгкxжсЕФжБЯпгыетИіЖўДЮКЏЪ§ЕФЭМЯѓНЛгкЕуEЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуPЕФКсзјБъЮЊxЃЌЧѓЯпЖЮPEЕФГЄЃЈгУКЌx ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉЕуDЮЊжБЯпABгыетИіЖўДЮКЏЪ§ЭМЯѓЖдГЦжсЕФНЛЕуЃЌШєвдЕуPЁЂEЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃЌЧыЧѓГіPЕуЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=![]() ЃЈxЉ1ЃЉ2Љ2ЃЛЃЈ2ЃЉPE=Љ
ЃЈxЉ1ЃЉ2Љ2ЃЛЃЈ2ЃЉPE=Љ![]() x2+
x2+![]() xЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ
xЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ![]() Љ1ЃЌ
Љ1ЃЌ![]() ЃЉЛђЃЈ1+
ЃЉЛђЃЈ1+![]() ЃЌ
ЃЌ![]() Љ1ЃЉЃЎ
Љ1ЃЉЃЎ
ЁОНтЮіЁП
(1)РћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪН.(2)ЯШЧѓГіжБЯпABЗНГЬЃЌдйЧѓГіPEГЄ.(3)РћгУЯрЫЦЕФаджЪЃЌСаБШР§ЪНЃЌдйДњШыЃЌНтЗНГЬЃЌПЩЧѓГіPЕузјБъ.
ЃЈ1ЃЉЩшЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=aЃЈxЉ1ЃЉ2Љ2ЃЌ
ЁпAЃЈ3ЃЌ0ЃЉдкХзЮяЯпЩЯЃЌ
Ёр0=aЃЈ3Љ1ЃЉ2Љ2
Ёрa=![]() ЃЌ
ЃЌ
Ёрy=![]() ЃЈxЉ1ЃЉ2Љ2ЃЌ
ЃЈxЉ1ЃЉ2Љ2ЃЌ
ЃЈ2ЃЉХзЮяЯпгыyжсНЛЕуBЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊy=kx+mЃЌ
Ёр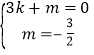 ,
,
Ёр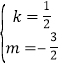 ,
,
ЁржБЯпABЕФНтЮіЪНЮЊy=![]() .
.
ЁпPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌ
ЁрPЕузјБъЮЊЃЈxЃЌ![]() xЉ
xЉ![]() .ЃЉЃЎЃЈ0ЃМxЃМ3ЃЉ
.ЃЉЃЎЃЈ0ЃМxЃМ3ЃЉ
гЩЬтвтПЩжЊPEЁЮyжсЃЌЁрEЕузјБъЮЊЃЈxЃЌ![]() x2ЉxЉ
x2ЉxЉ![]() ЃЉЃЌ
ЃЉЃЌ
Ёп0ЃМxЃМ3ЃЌ
ЁрPE=ЃЈ![]() .ЃЉЉЃЈ
.ЃЉЉЃЈ![]() x2ЉxЉ
x2ЉxЉ![]() ЃЉ=Љ
ЃЉ=Љ![]() x2+
x2+![]() .
.
ЃЈ3ЃЉгЩЬтвтПЩжЊDЕуКсзјБъЮЊx=1ЃЌгжDЕудкжБЯпABЩЯЃЌ
ЁрDЕузјБъЃЈ1ЃЌЉ1ЃЉЃЎ
ЕБЁЯEDP=90ЁуЪБЃЌЁїAOBЁзЁїEDPЃЌ
Ёр![]() .
.
Й§ЕуDзїDQЁЭPEгкQЃЌ
ЁрxQ=xP=xЃЌyQ=Љ1ЃЌ
ЁрЁїDQPЁзЁїAOBЁзЁїEDPЃЌ
Ёр![]() ,
,
гжOA=3ЃЌOB=![]() ЃЌAB=
ЃЌAB=![]() ,
,
гжDQ=xЉ1ЃЌ
ЁрDP=![]() ЃЈxЉ1ЃЉЃЌ
ЃЈxЉ1ЃЉЃЌ
Ёр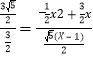 ,
,
НтЕУЃКx=Љ1ЁР![]() ЃЈИКжЕЩсШЅЃЉЃЎ
ЃЈИКжЕЩсШЅЃЉЃЎ
ЁрPЃЈ![]() Љ1ЃЌ
Љ1ЃЌ![]() ЃЉЃЈШчЭМжаЕФP1ЕуЃЉЃЛ
ЃЉЃЈШчЭМжаЕФP1ЕуЃЉЃЛ
ЂкЕБЁЯDEP=90ЁуЪБЃЌЁїAOBЁзЁїDEPЃЌ
Ёр![]() .
.
гЩЃЈ2ЃЉPE=Љ![]() x2+
x2+![]() .ЃЌDE=xЉ1ЃЌ
.ЃЌDE=xЉ1ЃЌ
Ёр![]()
НтЕУЃКx=1ЁР![]() ЃЌЃЈИКжЕЩсШЅЃЉЃЎ
ЃЌЃЈИКжЕЩсШЅЃЉЃЎ
ЁрPЃЈ1+![]() ЃЌ
ЃЌ![]() Љ1ЃЉЃЈШчЭМжаЕФP2ЕуЃЉЃЛ
Љ1ЃЉЃЈШчЭМжаЕФP2ЕуЃЉЃЛ
злЩЯЫљЪіЃЌPЕузјБъЮЊЃЈ![]() Љ1ЃЌ
Љ1ЃЌ![]() ЃЉЛђЃЈ1+
ЃЉЛђЃЈ1+![]() ЃЌ
ЃЌ![]() Љ1ЃЉЃЎ
Љ1ЃЉЃЎ

ЁОЬтФПЁПЪЁЩфЛїЖгЮЊДгМзЁЂввСНУћдЫЖЏдБжабЁАЮвЛШЫВЮМгШЋЙњБШШќЃЌЖд
ЫћУЧНјааСЫСљДЮВтЪдЃЌВтЪдГЩМЈШчЯТБэЃЈЕЅЮЛЃКЛЗЃЉЃК
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ | ЕкЮхДЮ | ЕкСљДЮ | |
Мз | 10 | 8 | 9 | 8 | 10 | 9 |
вв | 10 | 7 | 10 | 10 | 9 | 8 |
ЃЈ1ЃЉИљОнБэИёжаЕФЪ§ОнЃЌМЦЫуГіМзЕФЦНОљГЩМЈЪЧ ЛЗЃЌввЕФЦНОљГЩМЈЪЧ ЛЗЃЛ
ЃЈ2ЃЉЗжБ№МЦЫуМзЁЂввСљДЮВтЪдГЩМЈЕФЗНВюЃЛ
ЃЈ3ЃЉИљОнЃЈ1ЃЉЁЂЃЈ2ЃЉМЦЫуЕФНсЙћЃЌФуШЯЮЊЭЦМіЫВЮМгШЋЙњБШШќИќКЯЪЪЃЌЧыЫЕУїРэгЩЃЎ
ЃЈМЦЫуЗНВюЕФЙЋЪНЃКs2ЃН![]() Ѓл
Ѓл![]() ЃнЃЉ
ЃнЃЉ