题目内容
【题目】从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调查结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息.
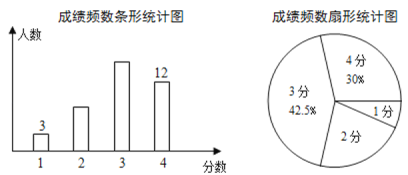
(1)求共抽取多少名学生;
(2)求抽取的所有学生成绩的众数,中位数;
(3)求抽取的所有学生成绩的平均数.
【答案】(1)40;(2)3分,3分;(3)抽取的所有学生成绩的平均数为2.95分
【解析】
(1)从两个统计图可得,“4分”的有12人,占调查人数的30%,可求出调查人数;
(2)根据中位数、众数的意义,求出出现次数最多的数和处在中间位置的数;
(3)根据加权平均数的意义,计算平均数即可.
解:(1)依题意得,共抽取学生12÷30%=40(人)
(2)由统计图可知:抽取的所有学生成绩的出现次数最多的是3分,因此众数是3分,
将成绩从从小到大排列后处在第20、21位两个数都是3分,因此中位数是3分,
(3)3分的学生人数为40×42.5%=17人,2分的人数有40﹣3﹣17﹣12=8人,
抽取的所有学生成绩的平均数是:(1×3+2×8+3×17+4×12)÷40=2.95(分).
答:抽取的所有学生成绩的平均数为2.95分.

练习册系列答案
相关题目