��Ŀ����
����Ŀ���뾶Ϊ2cm������O�߳�Ϊ2cm��������ABCD��ˮƽֱ��l��ͬ�࣬��O��l�����ڵ�F��DC��l�ϣ�
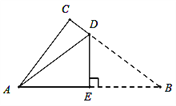
��1������B����һ������BE��EΪ�е㣮
����գ���ͼ1������A����O��ʱ����EBA�Ķ����� ��
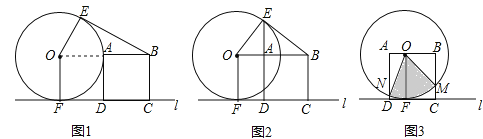
����ͼ2����E��A��D������ͬһֱ����ʱ�����߶�OA�ij���
��1����������ABCD�ı�AD��OF�غϵ�λ��Ϊ��ʼλ�ã������ƶ���������ͼ3��������BC.��OF�غ�ʱ�����ƶ���M��N�ֱ��DZ�BC��AD����O�Ĺ����㣬������MON������ķ�Χ.
���𰸡���1����30������OA=![]() -1����2��
-1����2��![]() ��S����MON�ܦ���
��S����MON�ܦ���
��������
������������������ߵ������Լ�ֱ�������ε����ʵó���EBA�Ķ������ɣ����������ߵ������Լ����ε����ʺ����������ε��ж������ʵó�![]() ,�������OA���ɣ�
,�������OA���ɣ�
��2������MON=n�����ó�S����MON=![]() n,�������ú��������Է�������N��M��A�ֱ���D��B��O�غ�ʱ��MN�������MN=DC=2ʱ��MN��С���ֱ�������ɣ�
n,�������ú��������Է�������N��M��A�ֱ���D��B��O�غ�ʱ��MN�������MN=DC=2ʱ��MN��С���ֱ�������ɣ�
�����������1���١��뾶Ϊ2cm������O�߳�Ϊ2cm��������ABCD��ˮƽֱ��l��ͬ�࣬����A����O��ʱ������B����һ������BE��EΪ�е㣬��OB=4��EO=2����OEB=90�������EBA�Ķ����ǣ�30����
����ͼ2����ֱ��l����O�����ڵ�F�����OFD=90������������ADCB�У���ADC=90����
��OF��AD����OF=AD=2�����ı���OFDAΪƽ���ı��Σ��ߡ�OFD=90������ƽ���ı���OFDAΪ���Σ���DA��AO����������ABCD�У�DA��AB����O��A��B������ͬһ��ֱ���ϣ���EA��OB���ߡ�OEB=��OAE��
���EOA�ס�BOE����![]() ����OE2=OAOB����ã�OA=-1��
����OE2=OAOB����ã�OA=-1��![]() ����OA��0����OA=
����OA��0����OA=![]() -1��
-1��
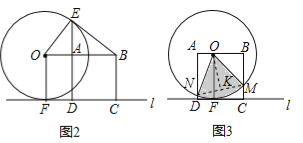
��2����ͼ3������MON=n����
S����MON=![]() ��cm2���� S��n�������������MONȡ���ֵʱ��S����MON�������MONȡ��Сֵʱ��S����MON��С����O����OK��MN��K�����MON=2��NOK��MN=2NK��
��cm2���� S��n�������������MONȡ���ֵʱ��S����MON�������MONȡ��Сֵʱ��S����MON��С����O����OK��MN��K�����MON=2��NOK��MN=2NK��
��Rt��ONK��sin��NOK=![]() �����NOK��NK��������������MON��MN�����������
�����NOK��NK��������������MON��MN�����������
����MN���ʱ��MON���MN��Сʱ��MON��С��
����N��M��A�ֱ���D��B��O�غ�ʱ��MN���MN=BD����MON=��BOD=90����S����MON���=����cm2����
����MN=DC=2ʱ��MN��С����ON=MN=OM�����NOM=60����S����MON��С=![]() ��cm2���� ��
��cm2���� ��![]() ��S����MON�ܦ���
��S����MON�ܦ���