Question

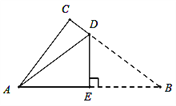
【题目】如图所示，是一张直角三角形的纸片，两直角边AC＝6㎝，BC＝8㎝，现将△ABC折叠，使点B与点A重合，折痕为DE，则AD的长为（ ）

A. 4㎝ B. 5㎝ C. 6㎝ D. ㎝

Answer 1

【答案】D

【解析】分析：首先设AD=xcm，由折叠的性质得：BD=AD=xcm，又由BC=8cm，可得CD=8-x（cm），然后在Rt△ACD中，利用勾股定理即可列出方程，解方程即可求得AD的长.

本题解析: 设AD=xcm，

由折叠的性质得：BD=AD=xcm,

∵在Rt△ABC中，AC=6cm，BC=8cm，

∴CD=BCBD=8x(cm)，AB=10cm，

在Rt△ACD中,AC +CD=AD，

即：6+(8x) =x，

解得：x=.故选D.