题目内容
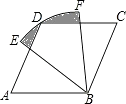
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

【答案】(1)见解析;(2)AB=2+![]() .
.
【解析】
(1)由旋转的性质可得∠BAC=∠CDF,可证DF垂直平分AC,可得AE=CE;
(2)由全等三角形的性质可得BE=CE=![]() ,由勾股定理可求CE=AE=2,即可求AB的长.
,由勾股定理可求CE=AE=2,即可求AB的长.
(1)∵将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,
∴△ABC≌△DBE,
∴∠BAC=∠CDF,
∵∠BAC+∠ACB=90°,
∴∠CDF+∠ACB=90°,
∴DF⊥AC,且点F是AC中点,
∴DF垂直平分AC,
∴AE=CE;
(2)∵△ABC≌△DBE,
∴BE=CE=![]() ,
,
∴CE=AE=2,
∴AB=AE+BE=2+![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目