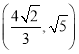Question

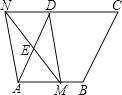
【题目】如图是某市民健身广场的平面示意图，它是由6个正方形拼成的长方形，已知中间最小的正方形的边长是1米；

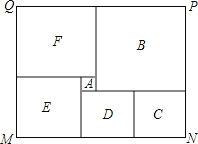
（1）若设图中最大正方形的边长是米，请用含的代数式分别表示出正方形的边长

（2）观察图形的特点可知，长方形相对的两边是相等的(即， )请根据以上结论，求出的值

（3）现沿着长方形广场的四条边铺设下水管道，由甲、乙工程队单独铺设分别需要10天、15天完成，如果两队从同一位置开始，沿相反的方向同时施工2天后，因甲队另有任务，余下的工程由乙队单独施工，还要多少天完成?

Answer 1

【答案】（1）F的边长为（x-1）米；C的边长为米；E的边长为（x-2）米；（2）7；（3）10

【解析】

（1）若设图中最大正方形B的边长是x米，最小的正方形的边长是1米，从图中可看出F的边长为（x-1）米，C的边长为，E的边长为（x-1-1），即可得到答案；

（2）根据长方形相对的两边是相等的（如图中的MN和P Q）．请根据这个等量关系，求出x的值；

（3）根据工作效率×工作时间=工作量这个等量关系且完成工作，工作量就为1，可列方程求解．

解：（1）若设图中最大正方形B的边长是x米，最小的正方形的边长是1米．

∴F的边长为：（x-1）米，

∴C的边长为：米，

∴E的边长为：x-1-1=（x-2）米；

（2）∵MQ=PN，

∴x-1+x-2=x+，

解得：x=7，

∴x的值为7；

（3）设余下的工程由乙队单独施工，还要x天完成．

∴（+）×2+x=1，

解得：x=10．

答：余下的工程由乙队单独施工，还要10天完成．