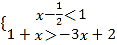题目内容
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,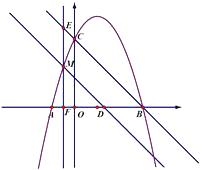
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1,S2 ,当BD=1时,请求S2-S1的值.
【答案】
(1)解:∵抛物线 y=x2+2x+3 与x轴的交点为A,B(点A在点B的左侧),
∴令y=0,即x2+2x+3 =0,
∴x1=-1,x2=3,
∴A(-1,0) ,B(3,0),
又∵抛物线与y轴的交点为C,
∴C(0,3),
(2)解:设BC的函数解析式为y=kx+b,
∵ B(3,0), C(0,3),
∴![]() ,
,![]() ,
,
∴BC的函数解析式为:y=-x+3,
∵点M是抛物线上A,C之间的一个动点,
∴设 M(m,m2+2m+3) (-1![]() m
m![]() 0),则 E(m,m+3),F(m,0),
0),则 E(m,m+3),F(m,0),
∴EF=-m+3,MF=m2+2m+3,
又∵M为EF中点,
∴ 2(m2+2m+3)=m+3 ,
∴ m1=3,m2=![]() ,
,
又∵-1![]() m
m![]() 0,
0,
∴m=![]() ,
,
∴F(-![]() ,0),
,0),
∴BF=3-(-![]() )=
)=![]() ,
,
又∵MD∥BC,
∴D为BF的中点,
∴ BD=![]() BF=
BF=![]() ×
×![]() =
=![]() .
.
(3)解:由图形可知,D在B点左侧,当BD=1时,D点坐标为(2,0),
由(2)知BC的函数解析式为:y=-x+3,
又∵MD∥BC,
∴MD的函数解析式为: y=x+2 .
∴![]() ,
,
解得: x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴M (![]() ,
,![]() ) ,E (
) ,E (![]() ,
,![]() ) ,
) ,
∴ME=1,DF=![]() ,EF=
,EF=![]() .
.
∴ S2S1=![]() ×1×
×1×![]()
![]() ×1×
×1×![]() =
=![]() .
.
【解析】(1)根据抛物线 y=x2+2x+3 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,分别令x=0,y=0即可求出A ,B,C坐标.
(2)由B、C的坐标用待定系数法即可求得直线BC的解析式,由点M是抛物线上A,C之间的一个动点,可设 M(m,m2+2m+3) (-1![]() m
m![]() 0),则 E(m,m+3),F(m,0),从而得到EF,MF的长,再由M为EF中点可得关于m的关系式,从而求出m,得出BF的长,再由MD∥BC,根据三角形中位线定理得出D为BF的中点,即BD=
0),则 E(m,m+3),F(m,0),从而得到EF,MF的长,再由M为EF中点可得关于m的关系式,从而求出m,得出BF的长,再由MD∥BC,根据三角形中位线定理得出D为BF的中点,即BD=![]() BF即可求得其值.
BF即可求得其值.
(3)由图形可知,D在B点左侧,当BD=1时,D点坐标为(2,0),由(2)知BC的函数解析式为:y=-x+3,根据MD∥BC得出MD的函数解析式为: y=x+2 ;再将MD解析式和抛物线联立求出M点坐标,从而得出E点坐标,由坐标得出ME,DF ,EF的长;再根据三角形面积公式得出S2S1值.
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.

【题目】根据表中的信息判断,下列语句中正确的是( )
x | 15 | 15.1 | 15.2 | 15.3 | 15.4 | 15.5 | 15.6 | 15.7 | 15.8 | 15.9 | 16 |
x2 | 225 | 228.01 | 231.04 | 234.09 | 237.16 | 240.25 | 243.36 | 246.49 | 249.64 | 252.81 | 256 |
A.![]()
B.235的算术平方根比15.3小
C.只有3个正整数n满足15.5![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?