Question

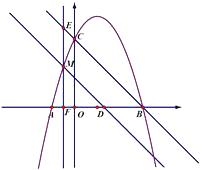
【题目】如图，在某场足球比赛中，球员甲从球门底部中心点O的正前方10m处起脚射门，足球沿抛物线飞向球门中心线；当足球飞离地面高度为3m时达到最高点，此时足球飞行的水平距离为6m．已知球门的横梁高为2.44m．

（1）在如图所示的平面直角坐标系中，问此飞行足球能否进球门？（不计其它情况）
（2）守门员乙站在距离球门2m处，他跳起时手的最大摸高为2.52m，他能阻止球员甲的此次射门吗？如果不能，他至少后退多远才能阻止球员甲的射门？

Answer 1

【答案】
（1）解：抛物线的顶点坐标是（4，3），

设抛物线的解析式是：y=a（x-4）2+3，

把（10，0）代入得36a+3=0，

解得a=- ，

则抛物线是y=- （x-4）2+3，

当x=0时，y=- ×16+3=3- = ＜2．44米，

故能射中球门；

（2）解：当x=2时，y=- （2-4）2+3= ＞2．52，

∴守门员乙不能阻止球员甲的此次射门，

当y=2．52时，y=- （x-4）2+3=2．52，

解得：x1=1．6，x2=6．4（舍去），

∴2-1．6=0．4（m），

答：他至少后退0．4m，才能阻止球员甲的射门．

【解析】（1） 抓住题中关键的已知条件可得出抛物线的顶点坐标为（4，3）且图像经过（10，0），利用待定系数法求出函数解析式即可。
（2）求出当x=2时对应的函数值，再与2．52比较大小，即可得出答案；再求出当y=2.52时对应的自变量的值，通过计算得出结果即可。