��Ŀ����
����Ŀ�����壺������������ʽ��![]() ��
��![]() ��������ʽ��
��������ʽ��![]() ������һ���⣬���Dz���ʽ��
������һ���⣬���Dz���ʽ��![]() ��һ���⣬��Ʋ���ʽ��
��һ���⣬��Ʋ���ʽ��![]() Ϊ����ʽ��
Ϊ����ʽ��![]() �ġ��Ӽ������磺����ʽ�飺
�ġ��Ӽ������磺����ʽ�飺![]() �ǣ�
�ǣ�![]() �ġ��Ӽ�����
�ġ��Ӽ�����
��1��������ʽ�飺![]() ��
��![]() �����в���ʽ��_________�Dz���ʽ��
�����в���ʽ��_________�Dz���ʽ��![]() �ġ��Ӽ�������
�ġ��Ӽ�������![]() ��
��![]() ����
����
��2��������![]() �IJ���ʽ��
�IJ���ʽ��![]() �Dz���ʽ��
�Dz���ʽ��![]() �ġ��Ӽ�������
�ġ��Ӽ�������![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��
��3����֪![]() Ϊ������ȵ�����������
Ϊ������ȵ�����������![]() ��
��![]() ��������������ʽ�飺
��������������ʽ�飺![]() ��
��![]() ��
��![]() ���㣺
���㣺![]() ��
��![]() �ġ��Ӽ�����
�ġ��Ӽ�����![]() ��
��![]() �ġ��Ӽ�������
�ġ��Ӽ�������![]() ��ֵΪ__________��
��ֵΪ__________��
��4����֪����ʽ��![]() �н⣬��
�н⣬��![]() �Dz���ʽ��
�Dz���ʽ��![]() �ġ��Ӽ�������д��
�ġ��Ӽ�������д��![]() ��
��![]() �����������________________��
�����������________________��
���𰸡�A ![]() -4
-4 ![]()
��������
��1���ȷֱ��������ʽ��A��B�Ľ⼯����������Ŀ�е��¶����жϼ��ɣ�
��2�����������ʽ��![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ���ٸ��ݶ����֪����ʽ��
���ٸ��ݶ����֪����ʽ��![]() �Ľ⼯��
�Ľ⼯��![]() ���ڲ������ɵó�a��ֵ��
���ڲ������ɵó�a��ֵ��
��3���ȸ����¶������a��b��c��d��ֵ���ٴ��뼴�ɣ�
��4�����������ʽ��M�Ľ⼯���ٸ����¶����ɣ�
�⣺��1����![]() �Ľ⼯Ϊ��
�Ľ⼯Ϊ��![]() ��
��![]() �Ľ⼯Ϊ��
�Ľ⼯Ϊ��![]() ��
��![]() �Ľ⼯Ϊ��
�Ľ⼯Ϊ��![]() ��
��
���ʽ��A�Dz���ʽ��M�ġ��Ӽ�����
�ʴ�Ϊ��A��
��2���߲���ʽ��![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ���Ҳ���ʽ��
���Ҳ���ʽ��![]() �Ľ⼯��
�Ľ⼯��![]() ���ڲ���
���ڲ���
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3����![]() Ϊ������ȵ�����������
Ϊ������ȵ�����������![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ���㣺
���㣺![]() ��
��![]() �ġ��Ӽ�����
�ġ��Ӽ�����![]() ��
��![]() �ġ��Ӽ�����
�ġ��Ӽ�����
��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��-4��
��4��������ʽ��M�����ã�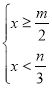 ��
��
�߲֡���ʽ��M�н⣬
��![]() ��
��
��![]() �Dz���ʽ��
�Dz���ʽ��![]() �ġ��Ӽ�����
�ġ��Ӽ�����
��![]() ����
����![]() ��
��
�ʴ�Ϊ��![]() ��
��