题目内容
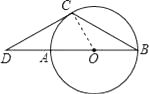
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
【答案】
(1)解:连接OC.
∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
∴∠COD=∠B+∠OCB=60°,
∵∠BDC=30°,
∴∠BDC+∠COD=90°,DC⊥OC,
∵BC是弦,
∴点C在⊙O上,
∴DC是⊙O的切线,点C是⊙O的切点;
(2)解:∵AB=2,
∴OC=OB= ![]() =1,
=1,
∵在Rt△COD中,∠OCD=90°,∠D=30°,
∴DC= ![]() OC=
OC= ![]() .
.
【解析】(1)连接OC,根据已知易证明∠COD=60°,再利用三角形内角和定理求出∠DCO的度数,即可证得DC⊥OC,根据切线的判定定理即可证得结论。
(2)根据已知求出OC的长,然后在Rt△COD中,利用解直角三角形求出DC的长即可。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目