题目内容
【题目】操作与证明:
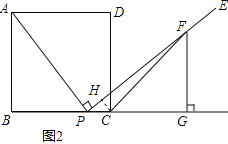
如图1,已知P是矩形ABCD的边BC上的一个点(P与B、C两点不重合),过点P作射线PE⊥AP,在射线PE上截取线段PF,使得PF=AP.
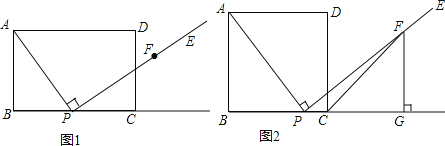
(1)过点F作FG⊥BC交射线BC点G.(尺规作图,保留痕迹,不写作法)
(2)求证:FG=BP.
探究与计算:
(3)如图2,若AB=BC,连接CF,求∠FCG的度数;
(4)在(3)的条件下,当![]() =
=![]() 时,求sin∠CFP的值.
时,求sin∠CFP的值.
【答案】(1)见解析;(2)见解析;(3)∠FCG=45°;(4)![]() .
.
【解析】
试题分析:(1)利用作一个角等于已知角的方法,即可作出所求直线;
(2)易求得∠BAP=∠GPF,∠ABP=∠PGF=90°,又由AP=PF,即可证得△ABP≌△PGF,继而证得结论;
(3)首先证得FG=CG,即可得△FCG是等腰直角三角形,继而求得答案;
(4)首先作CH⊥PF于H,易证得△PHC∽△PGF,由相似三角形的对应边成比例,可得![]() ,然后设BP=3a,则PC=a,PG=4a,FG=CG=3a,分别求得FC,HC,继而求得答案.
,然后设BP=3a,则PC=a,PG=4a,FG=CG=3a,分别求得FC,HC,继而求得答案.
(1)解:如图1所示:
(2)证明:∵PE⊥AP,
∴∠APE=90°.
∴∠APB+∠GPF=90°,
又∵∠APB+∠BAP=90°,
∴∠BAP=∠GPF,
又∵FG⊥BC,
∴∠ABP=∠PGF=90°,
在△ABP与△PGF中,
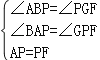 ,
,
∴△ABP≌△PGF(AAS).
∴FG=BP;
(3)解:由(2)知AB=PG,
∵AB=BC,
∴BC=PG.
∴BC﹣PC=PG﹣PC.
∴BP=CG,
又∵FG=BP,
∴FG=CG.
又∵∠CGF=90°,
∴∠FCG=45°;
(4)解:如图2,作CH⊥PF于H,
∵∠HPC=∠GPF,∠CHP=∠FGP=90°,
∴△PHC∽△PGF.
∴![]() ,
,
根据![]() ,
,
设BP=3a,则PC=a,PG=4a,FG=CG=3a,
∴PF=![]() =5a,CF=
=5a,CF=![]() =3
=3![]() a,
a,
∴![]() .
.
∴HC=![]() a,
a,
∴sin∠CFP= =
=![]() .
.