题目内容
【题目】如图，已知二次函数
的图象经过
、
、
三点．
（1）求该二次函数的解析式；
（2）若点M是该二次函数图象上的一点，且满足
，求点M的坐标；
（3）点P是该二次函数图象上位于一象限上的一动点，连接PA分别交BC，y轴与点E、F，若
、
的面积分别为
、
，求
的最小值．
【答案】（1）
（2）
或（－5，－18）
（3）
【解析】
（1）已知三点坐标，代入二次函数解析式，得三元一次方程组，可求得二次函数解析式.
（2）已知二次函数解析式，可求得B点坐标为（4，0）当点M在x轴上方时，过C作CM∥AB交抛物线于点M，四边形ABMC为等腰梯形，可求得满足条件的M点坐标.如果M点在x轴下方，先求出直线AC和直线BM的解析式，直线BM的解析式和抛物线的交点即为M点，联立方程求解.
（3）过点P作PH∥y轴交直线BC于点H，可设出P点坐标，从而可表示出PH的长，可表示出△PEB的面积，进一步可表示出直线AP的解析式，可求得F点的坐标，联立直线BC和PA的解析式，可表示出E点横坐标，从而可表示出△CEF的面积，再利用二次函数的性质可求得S2-S1的最小值．
（1）已知二次函数
的图象经过
、
、
三点
则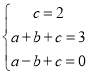
得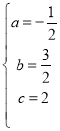
二次函数解析式为：
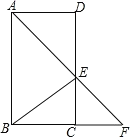
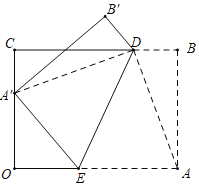
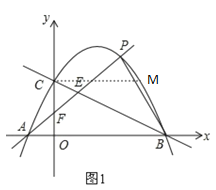
（２）当点M在x轴上方时，过C作CM∥AB交抛物线于点M，如图1
∵A、B关于对称轴对称，CM关于对称轴对称
∴四边形ABMC为等腰梯形
∴∠CAO=∠MBA，即点M满足条件
∴M(3，2)
当点M在x轴下方时
∵∠MBA=∠CAO
∴BM∥AC
∵C(0，2)，
∴可设直线AC解析式为y=kx+2，把A(1，0)代入可求得k=2，
∴直线AC解析式为y=2x+2，
∴可设直线BM解析式为y=2x+m，把B(4，0)代入可求得m=8，
∴直线BM解析式为y=2x8，
联立直线BM和抛物线解析式可得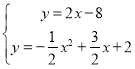
解得
或
∴M(5，18)
综上可知满足条件的点M的坐标为(3，2)或(5，18)；
（3）
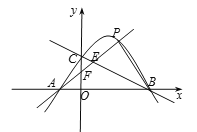
过点P作PH∥y轴交直线BC于点H，如图2，
设
由B、C两点的坐标可求得直线BC的解析式为y=
x+2
∴H(t，t+2)
∴PH=yPyH=
(t+2)=
设直线AP的解析式为y=px+q
∴
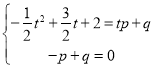
解得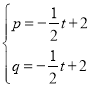
∴直线AP的解析式为
，令x=0可得
∴F(0，
)，
∴CF=2（）=
联立直线AP和直线BC解析式可得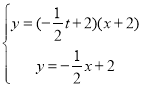
解得x=
，即E点的横坐标为
当
时，S2-S1的最小值为-
