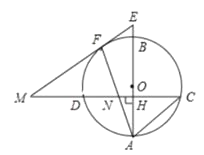
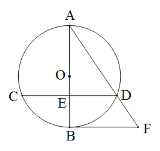
题目内容
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于x轴对称,点
关于x轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于x轴,直线l的二次对称点.
是点P关于x轴,直线l的二次对称点.
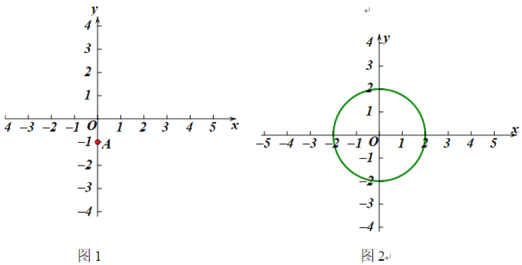
(1)如图1,点A(0,-1).
①若点B是点A关于x轴,直线![]() :x=2的二次对称点,则点B的坐标为 ;
:x=2的二次对称点,则点B的坐标为 ;
②点C (-4,1)是点A关于x轴,直线![]() :x=a的二次对称点,则a的值为 ;
:x=a的二次对称点,则a的值为 ;
③点D(-1,0)是点A关于x轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为 ;
的表达式为 ;
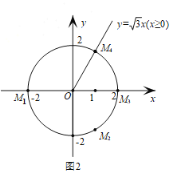
(2)如图2,O的半径为2.若O上存在点M,使得点M′是点M关于x轴,直线![]() :x = b的二次对称点,且点M′在射线
:x = b的二次对称点,且点M′在射线![]() (x≥0)上,b的取值范围是 ;
(x≥0)上,b的取值范围是 ;
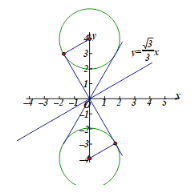
(3)E(0,t)是y轴上的动点,E的半径为2,若E上存在点N,使得点N′是点N关于x轴,直线![]() :
:![]() 的二次对称点,且点N′在x轴上,求t的取值范围.
的二次对称点,且点N′在x轴上,求t的取值范围.
【答案】(1)①(4,1),②-2,③y =- x;(2)b的取值范围是-1≤b≤![]() ;(3)-4≤t≤4
;(3)-4≤t≤4
【解析】
(1)①根据题目中二次对称点的定义,可以求得点B的坐标;
②根据题目中二次对称点的定义,可以求得a的值;
③根据题目中二次对称点的定义,可以求得直线l3的表达式;
(2)根据题意可以画出相应的图形,利用分类讨论的方法即可解答本题;
(3)根据题意和对称的二次对称点的定义,根据题目中的图形,可以求得t的取值范围,本题得以解决.
解:(1)① 点B的坐标为 (4,1)
② a的值为-2
③直线l3的表达式为y =- x
(2)如图2,
设O与x轴的两个交点为![]() (-2,0),
(-2,0),![]() (2,0),
(2,0),
与射线![]() (x≥0)的交点为
(x≥0)的交点为![]() ,则
,则![]() 的坐标为(1,
的坐标为(1,![]() ).
).
![]() 关于x轴的对称点为
关于x轴的对称点为![]() .
.
当点M在![]() 的位置时,b=-1,
的位置时,b=-1,
当点M在![]() 的位置时,b=1,
的位置时,b=1,
当点M在![]() 的位置时,b=1,
的位置时,b=1,
当点M在劣弧![]() 上时(如图3),-1≤b≤1,
上时(如图3),-1≤b≤1,
当点M在劣弧![]() 上时(如图4),b的值比1大,当到劣弧
上时(如图4),b的值比1大,当到劣弧![]() 的中点时,达到最大值(如图5),最大值为
的中点时,达到最大值(如图5),最大值为![]() .综上,b的取值范围是-1≤b≤
.综上,b的取值范围是-1≤b≤![]() .
.

(3)∵x轴和直线![]() 关于直线
关于直线![]() 对称,
对称,
直线![]() 和直线
和直线![]() 关于x轴对称,
关于x轴对称,
∴E只要与直线![]() 和
和![]() 有交点即可.
有交点即可.
∴t 的取值范围是:-4≤t≤4
. 

 习题精选系列答案
习题精选系列答案