题目内容
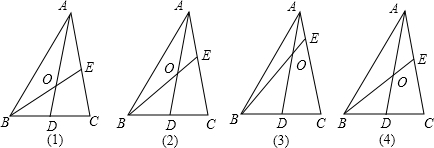
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD与点O,某学生在研究这一问题时,发现了如下事实,
①当
=
=
时,有
=
=
(如图1);
②当
=
=
时,有
=
=
(如图2);
③
=
=
时,有
=
=
(如图3);
如图4中,当
=
时,请你猜想
的一般结论,并证明你的结论(其中n为正整数).
①当
| AE |
| AC |
| 1 |
| 2 |
| 1 |
| 1+1 |
| AO |
| AD |
| 2 |
| 3 |
| 2 |
| 2+1 |
②当
| AE |
| AC |
| 1 |
| 3 |
| 1 |
| 1+2 |
| AO |
| AD |
| 2 |
| 4 |
| 2 |
| 2+2 |
③
| AE |
| AC |
| 1 |
| 4 |
| 1 |
| 1+3 |
| AO |
| AD |
| 2 |
| 5 |
| 2 |
| 2+3 |
如图4中,当
| AE |
| AC |
| 1 |
| 1+n |
| AO |
| AD |

猜想
=
.
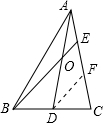
证明:过D作DF∥BE,
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=
EC.
∵
=
,
∴AE:(AE+2EF)=1:(1+n).
∴AE:EF=2:n.
∴AE:AF=2:(n+2),即
=
.
| AO |
| AD |
| 2 |
| n+2 |
证明:过D作DF∥BE,
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=
| 1 |
| 2 |
∵
| AE |
| AC |
| 1 |
| 1+n |
∴AE:(AE+2EF)=1:(1+n).
∴AE:EF=2:n.
∴AE:AF=2:(n+2),即
| AO |
| AD |
| 2 |
| n+2 |


练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目