题目内容
如图,在平面直角坐标系中,以坐标原点为圆心,半径为1的⊙O与x轴交于A、B两点,与y轴交于C、D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数关系式为_ __.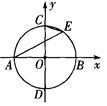

y=-x+1或y=x-1
试题分析:由题意可知,∠AEC=
 ∠AOC=45°;当∠ABF=∠AEC=45°时,只有点F与点C或D重合,根据待定系数法可求出直线BF对应的函数表达式.
∠AOC=45°;当∠ABF=∠AEC=45°时,只有点F与点C或D重合,根据待定系数法可求出直线BF对应的函数表达式.
根据圆周角定理得,∠AEC=
 ∠AOC=45°,
∠AOC=45°,∵∠ABF=∠AEC=45°,
∴点F与点C或D重合;
当点F与点C重合时,设直线BF解析式y=kx+b,

∴直线BF的解析式为y=-x+1,
当点F与点D重合时,同理可得y=x-1.
点评:解题的关键是读懂题意及图形,根据圆周角定理正确进行分类,同时熟练掌握待定系数法求解析式的方法.

练习册系列答案
相关题目

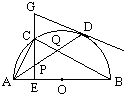

 ,OP=2,则AC的长是( )
,OP=2,则AC的长是( )


