题目内容
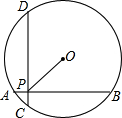
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD.⑤CB∥GD.
其中正确结论的个数是( )

A.1 B.2 C.3 D.4
其中正确结论的个数是( )

A.1 B.2 C.3 D.4
B
试题分析:连接OD,∵GD是切线∴OD⊥GD,又∵OD="OA," ∴∠DAO=∠ADO, ∵CE⊥AB, ∴∠DA0+∠APE=90°,∠ODA+∠ADG=90°,而∠APE=∠GPD, ∴∠GDP=∠GPD, ∴GP="GD.." ∵AB为直径∴∠ACB=90°,∴∠ACP+∠PCQ=90°,∵∠BAC+∠ABC=90°∴∠BCE=∠CAE又点C为AD弧中点,∴∠CBD=∠CAD, ∴∠ACP=∠PAC,同理∠PCQ=∠PQC, ∴点P为AQ的中点,∴点P是△ACQ的外心,由已知得C,D不是AB弧的三等份的点,所以,①,②,⑤不正确,只有③,④正确。
点评:熟知上述性质定义,本题问较多,很复杂,需细心审题,从已知入手,还需要做辅助线,本题由一定的难度,属于中档题。

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目

 cm2.
cm2.
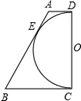
 的圆心在x轴上,且经过
的圆心在x轴上,且经过 、
、 两点,抛物线
两点,抛物线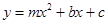 (m>0)经过A、B两点,顶点为P。
(m>0)经过A、B两点,顶点为P。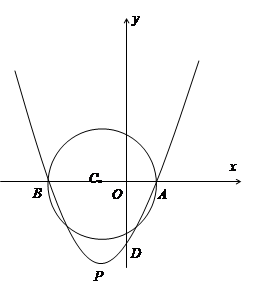
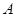 、
、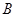 、
、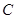 三根木柱,使得
三根木柱,使得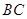 长为120米,
长为120米,