题目内容
【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:
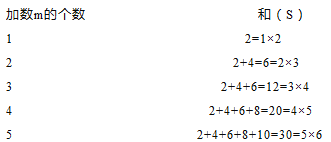
(1)和S与加数的个数m之间的数量关系为S= (用含m 的代数式表示);
(2)按此规律计算(写出必要的演算过程):
(i)2+4+6+┈+300 的值;
(ii)162+164+166+┈+400 的值.
【答案】(1)S=m(m+1);(2)(i)22650;(ii)33720.
【解析】试题分析:(1)隐含规律:从2开始的连续的几个偶数的和等于最后一个偶数的一半与最后一个偶数的一半大1 的数的积
(2)①直接代入(1)的公式计算即可
②将“162+164+166+…+400”变为“(2+4+6+8+…+162+164+…+400)-(2+4+6+8+…+158+160)”代公式计算即可.
试题解析:(1)S=m(m+1)
(2)(i)2+4+6+…+300=![]() ×(
×(![]() +1)=150×151=22650
+1)=150×151=22650
(ii)∵2+4+6+8+…+162+164+…+400=200×201=40200,
2+4+6+8+…+158+160=80×81=6480,
∴162+164+166+…+400
=(2+4+6+8+…+162+164+…+400)-(2+4+6+8+…+158+160)
=40200-6480
=33720.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目