题目内容
【题目】如图，已知四边形ABCD中，∠D＝100°，AC平分∠BCD，且∠ACB＝40°，∠BAC＝70°.
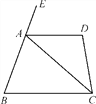
(1)AD与BC平行吗？试写出推理过程；
(2)求∠DAC和∠EAD的度数.
【答案】(1)AD与BC平行；（2）70°.
【解析】试题分析：（1）根据角平分线的定义求出∠BCD，得到∠D+∠BCD=180°，根据平行线的判定即可推理．
（2）根据平行线的性质求出∠DAC，代入∠EAD=180°-∠DAC-∠BAC求出即可．
试题解析：
（1）AD∥BC ，
∵AC平分∠BCD，∠ACB=40°，
∴∠BCD=2∠ACB=80° ，
∵∠D=100°，
∴∠D+∠BCD=180° ，
∴AD∥BC.
（2）∵AD∥BC，∠ACB=40°，
∴∠DAC=∠ACB=40°，
∵∠BAC=70°，
∴∠DAB=∠DAC+∠BAC=40°+70°=110° ，
∴∠EAD=180°-∠DAB=180°-110°=70°.
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
【题目】有一根弹簧原长10厘米，挂重物后（不超过50克），它的长度会改变，请根据下面表格中的一些数据回答下列问题：
质量（克） | 1 | 2 | 3 | 4 | ……n |
伸长量（厘米） | 0．5 | 1 | 1．5 | 2 | …… |
总长度（厘米） | 10．5 | 11 | 11．5 | 12 | …… |
（1）要想使弹簧伸长5厘米，应挂重物多少克？
（2）当所挂重物为x克时，用代数式表示此时弹簧的总长度．
（3）当x=30克时，求此时弹簧的总长度．
