题目内容
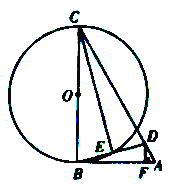
【题目】(2016贵州省毕节市第26题)如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
(1)、求证:AB是☉O的切线;(2)、若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
【答案】(1)、证明过程见解析;(2)、4![]()
【解析】
试题分析:(1)、根据CB=CD得出∠CBD=∠CDB,然后结合∠BCD=2∠ABD得出∠ABD=∠BCE,从而得出∠CBD+∠ABD=∠CBD+∠BCE=90°,然后得出切线;(2)、根据Rt△AFD和Rt△BFD的性质得出AF和DF的长度,然后根据△ADF和△ACB相似得出相似比,从而得出BC的长度.
试题解析:(1)、∵CB=CD ∴∠CBD=∠CDB 又∵∠CEB=90° ∴∠CBD+∠BCE=∠CDE+∠DCE
∴∠BCE=∠DCE且∠BCD=2∠ABD ∴∠ABD=∠BCE ∴∠CBD+∠ABD=∠CBD+∠BCE=90°
∴CB⊥AB垂足为B 又∵CB为直径 ∴AB是⊙O的切线.
(2)、∵∠A=60°,DF=![]() ∴在Rt△AFD中得出AF=1 在Rt△BFD中得出DF=3
∴在Rt△AFD中得出AF=1 在Rt△BFD中得出DF=3
∵∠ADF=∠ACB ∠A=∠A ∴△ADF∽△ACB ∴![]() 即
即![]() 解得:CB=4
解得:CB=4![]()

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目