题目内容
【题目】某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,
表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | |
压强增加值 Y(kpa) | 0 | 9.5 | 18 | 25.5 | 32 | 37.5 | 42 |
(1)根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);
(2)y与t之问是否存在函数关系?若是,请求出函数关系式;否则请说明理由;
(3)①在该模式下,压强P的最大值是多少?
②当t分别为,t1,t2(t1<t2)时,对应y的值分别为y1 ,y2 , 请比较![]() 与
与![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
【答案】(1)见解析;(2)![]() ;(3)①p=150,②
;(3)①p=150,②![]() >
>![]() 实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.
实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.
【解析】(1)根据表中提供的数据,在直角坐标系中,描出各个点即可;
(2)观察点的坐标特点,图像过(0,0),因此设y与t之间的函数关系式为:y=at2+bt,求出函数解析式,再验证其它的点是否满足此函数解析式,即可求解;
(3)①根据(2)中的函数解析式,求出顶点坐标,得出y的最大值,再根据y=p-100,可求出压强p的最大值;②先求出y1与t1的比值及y2与t2的比值,根据t1<t2即可求解.
(1)如图
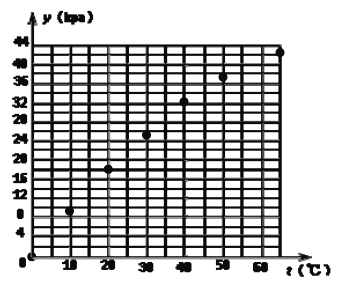
(2)∵图像经过(0,0)(10,9.5),(20,18),
∴设y与t之间的函数关系式为:y=at2+bt,
∴![]() ,
,
![]()
解之: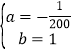 ,
,
∴y与t的函数关系为:![]() ,
,
经验证:其它的各个点都满足该函数解析式.
(3)解:①![]() ,
,
当t=100,y有最大值是50,
∵y=p-100=50,
∴p=150,
在该模式下,压强P的最大值是150;
②当t分别为:t1 ,t2(t1<t2)时,![]() ,
,![]() ,
,
∵t1<t2
∴![]() >
>![]()
实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.

【题目】八(6)班为从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评.其中,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表;另全班50位同学参与民主测评进行投票,结果如下图:
![]()
A | B | C | D | E | |
甲 | 89 | 91 | 92 | 94 | 93 |
乙 | 90 | 86 | 85 | 91 | 94 |

规定: 演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的平均分;
(2)民主测评统计图中a= ,b= ;
(3)求甲、乙两位选手的民主测评得分;
(4)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长?