题目内容
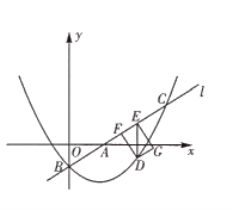
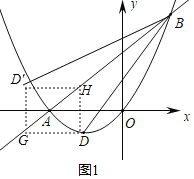
【题目】如图,抛物线y=ax2+bx(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2,顶点为D.
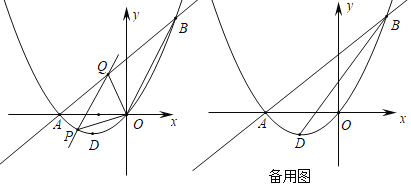
(1)填空:抛物线的解析式为 ,顶点D的坐标为 ,直线AB的解析式为 ;
(2)在直线AB左侧抛物线上存在点E,使得∠EBA=∠ABD,求E的坐标;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
【答案】(1)y=![]() x2+x;(﹣2,﹣1);y=x+4;(2)(﹣
x2+x;(﹣2,﹣1);y=x+4;(2)(﹣![]() ,
,![]() );(3)P(﹣2
);(3)P(﹣2![]() ,2﹣2
,2﹣2![]() ).
).
【解析】
(1)根据对称轴可求得A点坐标,再根据B点坐标,利用待定系数法即可求得抛物线以及一次函数解析式,再利用对称轴为x=﹣2可求得抛物线顶点坐标;
(2)证明四边形GDHD′为正方形,点D(-2,-1),则点G(-5,-1),则正方形的边长为3,则点D′(-5,2),求得直线BD′的解析式,与抛物线联立即可求解;
(3)证明四边形PQHO为平行四边形,则xQ-xP=xH-xO,即可求解.
解:(1)对称轴为直线x=﹣2,则点A(﹣4,0),
将点A、B的坐标代入抛物线表达式得![]() ,解得
,解得![]() .
.
故抛物线的表达式为:y=![]() x2+x…①,
x2+x…①,
当x=-2时,![]()
∴顶点D的坐标为:(﹣2,﹣1),
设直线AB的表达式为![]() ,
,
将点A、B的坐标代入一次函数表达式![]() ,解得
,解得![]() ,
,
所以,直线AB的表达式为:y=x+4…②,
故答案为:y=![]() x2+x;(﹣2,﹣1);y=x+4;
x2+x;(﹣2,﹣1);y=x+4;
(2)作点D关于AB的对称点D′,分别过点D、D′作x轴的平行线交直线AB与点G、H,
则![]() ,
,![]() ,
,
∵直线AB的解析式为y=x+4,![]() ∥x轴,
∥x轴,![]() ∥x轴,
∥x轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
则四边形GDHD′为正方形,
根据点D(﹣2,﹣1),可得点G(﹣5,﹣1),
所以,正方形的边长为3,
则点D′(﹣5,2),
设直线BD′的表达式为:![]() ,所以
,所以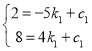 ,解得
,解得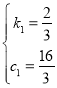 ,
,
所以,直线BD′的表达式为:y=![]() x+
x+![]() …③;
…③;
联立①③并解得:x=﹣![]() 或4(舍去),
或4(舍去),
故点E(﹣![]() ,
,![]() );
);
(3)取OB的中点H(2,4),则S△OQH=![]() S△OBQ,而S△POQ:S△BOQ=1:2,
S△OBQ,而S△POQ:S△BOQ=1:2,
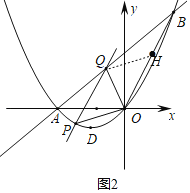
故S△OQH=S△POQ,
∵PQ∥OH,故PQ=OH(四边形PQHO为平行四边形),
则xQ﹣xP=xH﹣xO,
设点P(m,![]() m2+m),
m2+m),
直线OB的表达式为:y=2x,
则直线PQ的表达式为:y=2x+b1,将点P的坐标代入上式得![]() ,解得
,解得![]() ,
,
所以,直线PQ的表达式为:y=2x+![]() m2﹣m…④,
m2﹣m…④,
联立②④并解得:xQ=﹣![]() m2+m+4,
m2+m+4,
而xQ﹣xP=xH﹣xO,
即﹣![]() m2+m+4﹣m=2,
m2+m+4﹣m=2,
解得:m=![]() 或m=
或m=![]() (舍去),
(舍去),
故点P(﹣2![]() ,2﹣2
,2﹣2![]() ).
).

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】2019年10月10日傍晚18:10左右,江苏省无锡市山区312国道上海方向K135处,锡港路上跨桥出现桥面侧翻,造成3人死亡,2人受伤,尽管该事故原因初步分析为半挂牵引车严重超载导致桥梁发生侧翻,但是也引起了社会各界对桥梁设计安全性的担忧,我市积极开展对桥梁结构设计的安全性进行评估(已知:抗倾覆系数越高,安全性越强;当抗倾覆系数≥2.5时,认为该结构安全),现在重庆市随机抽取了甲、乙两个设计院,对其各自在建的或已建的20座桥梁项目进行排查,将得到的抗倾覆数据进行整理、描述和分析(抗倾覆数据用x表示,共分成6组:A.0≤x<2.5,B.2.5≤x<5.0,C.5.0≤x<7.5,D.7.5≤x<10.0,E.10.0≤x<12.5,F.12.5≤x<15),下面给出了部分信息;
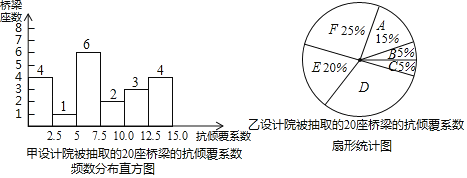
其中,甲设计院C组的抗倾覆系数是:7,7,7,6,7,7;
乙设计院D组的抗倾覆系数是:8,8,9,8,8,8;
甲、乙设计院分别被抽取的20座桥梁的抗倾覆系数统计表
设计院 | 甲 | 乙 |
平均数 | 7.7 | 8.9 |
众数 | a | 8 |
中位数 | 7 | b |
方差 | 19.7 | 18.3 |
根据以上信息解答下列问题:
(1)扇形统计图中D组数据所对应的圆心角是 度,a= ,b= ;
(2)根据以上数据,甲、乙两个设计院中哪个设计院的桥梁安全性更高,说明理由(一条即可): ;
(3)据统计,2018年至2019年,甲设计院完成设计80座桥梁,乙设计院完成设计120座桥梁,请估算2018年至2019年两设计院的不安全桥梁的总数.
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
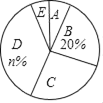
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?