Question

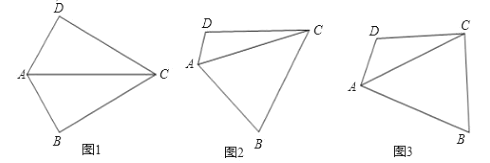
【题目】如图，以矩形ABCD对角线AC为底边作等腰直角△ACE，连接BE，分别交AD，AC于点F，N，CD＝AF，AM平分∠BAN．下列结论：①EF⊥ED；②∠BCM＝∠NCM；③AC＝EM；④BN2+EF2＝EN2；⑤AEAM＝NEFM，其中正确结论的个数是（　　）

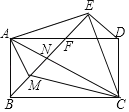
A.2B.3C.4D.5

Answer 1

【答案】C

【解析】

①正确，只要证明A，B，C，D，E五点共圆即可解决问题；

②正确，证明BE平分∠ABC，再证明点M是△ABC的内心即可；

③正确，证明∠EAM＝∠EMA可得EM=AE，即可解决问题；
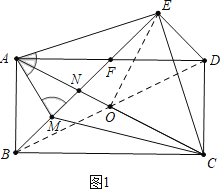
④正确．如图2中，将△ABN逆时针旋转90°得到△AFG，连接EG．想办法证明△GEF是直角三角形，利用勾股定理即可解决问题；
⑤错误．利用反证法证明即可．

解：如图1中，连接BD交AC于O，连接OE．

∵四边形ABCD是矩形，

∴OA＝OC＝OD＝OB，

∵∠AEC＝90°，

∴OE＝OA＝OC，

∴OA＝OB＝OC＝OD＝OE，

∴A，B，C，D，E五点共圆，BD是直径，

∴∠BED＝90°，

∴EF⊥ED，故①正确，

∵CD＝AB＝AF，∠BAF＝90°，

∴∠ABF＝∠AFB＝∠FBC＝45°，

∴BM平分∠ABC，

∵AM平分∠BAC，

∴点M是△ABC的内心，

∴CM平分∠ACB，

∴∠MCB＝∠MCA，故②正确，

∵∠EAM＝∠EAC+∠MAC，∠EMA＝∠BAM+∠ABM，∠ABM＝∠EAC＝45°，

∴∠EAM＝∠EMA，

∴EA＝EM，

∵△EAC是等腰直角三角形，

∴AC＝EA＝EM，故③正确，

如图2中，将△ABN绕点A逆时针旋转90°，得到△AFG，连接EG，

∵将△ABN绕点A逆时针旋转90°，得到△AFG，

∴∠NAB＝∠GAF，∠GAN＝∠BAD＝90°，AG＝AN，GF＝BN，

∵∠EAN＝45°，

∴∠EAG＝∠EAN＝45°，

∵AE＝AE，

∴△AEG≌△AEN（SAS），

∴EN＝EG，

∵∠AFG＝∠ABN＝∠AFB＝45°，

∴∠GFB＝∠GFE＝90°，

∴EG2＝GF2+EF2，

∴BN2+EF2＝EN2，故④正确，

不妨设AEAM＝NEFM，

∵AE＝EC，

∴，

∴只有△ECN∽△MAF才能成立，

∴∠AMF＝∠CEN，

∴CE∥AM，

∵AE⊥CE，

∴MA⊥AE（矛盾），

∴假设不成立，故⑤错误，

故选：C．