题目内容
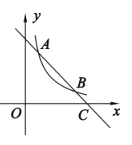
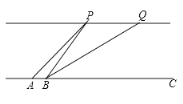
【题目】如图,![]() 、
、![]() 为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点
为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点![]() 处测得
处测得![]() ,再沿着河岸前进10米后到达
,再沿着河岸前进10米后到达![]() 点,在点
点,在点![]() 处测得
处测得![]() ,
,![]() .
.
(1)求河宽;
(2)该小组发现此时还可求得![]() 、
、![]() 之间的距离,请求出
之间的距离,请求出![]() 的长.(精确到0.1米)(参考数据:
的长.(精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)河宽40米;(2)![]() 米
米
【解析】
(1)过点P作PE⊥AC于点E,设河宽PE=x,然后利用锐角三角函数分别用x表示出AE和BE,然后列出方程即可求出结论;
(2)过点Q作QF⊥AC于点F,根据矩形的性质可得QF=PE=40米,PQ=EF,利用锐角三角函数即可求出BF,从而得出结论.
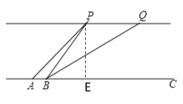
解:(1)过点P作PE⊥AC于点E,设河宽PE=x
在Rt△APE中,![]()
∴PE=AE=x
在Rt△BPE中,![]()
∴BE=![]()
∵AE-BE=AB,AB=10米
∴![]()
解得:x=40
答:河宽40米.
(2)过点Q作QF⊥AC于点F,易知四边形PEFQ为矩形
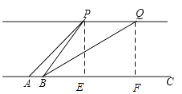
∴QF=PE=40米,PQ=EF
在Rt△BFQ中,![]()
∴BF=![]() 米
米
由(1)可知:BE=![]() 米
米
∴EF=BF-BE=(![]() -30)米
-30)米
∴PQ= EF=![]() -30≈
-30≈![]() 米
米

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
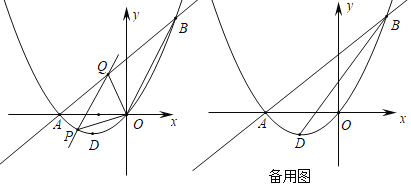
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.