题目内容
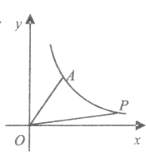
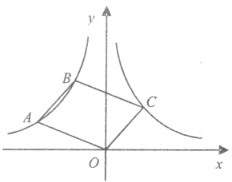
【题目】如图，点
，
在反比例函数
的图象上，连结
，
，以，为边作
，若点
恰好落在反比例函数
的图象上，此时的面积是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
连接AC，BO交于点E，作AG⊥x轴，CF⊥x轴，设点A（a，
），点C（m，
）（a＜0，m＞0），由平行四边形的性质和中点坐标公式可得点B[（a+m），（+）]，把点B坐标代入解析式可求a=-2m，由面积和差关系可求解．
解：如图，连接AC，BO交于点E，作AG⊥x轴，CF⊥x轴，
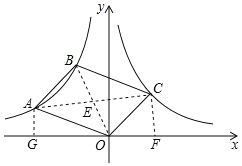
设点A（a，），点C（m，）（a＜0，m＞0），
∵四边形ABCO是平行四边形，
∴AC与BO互相平分，
∴点E（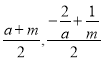
），
∵点O坐标（0，0），
∴点B[（a+m），（+）].
∵点B在反比例函数y=
（x＜0）的图象上，
∴
，
∴a=-2m，a=m（不合题意舍去），
∴点A（-2m，），
∴四边形ACFG是矩形，
∴S△AOC=
（+）（m+2m）--1=
，
∴OABC的面积=2×S△AOC=3.
故选：A．
【题目】某水果批发市场规定，一次购买苹果不超过100kg（包括100kg），批发价为5元，如果一次购买100kg以上苹果，超过100kg的部分苹果价格打8折．
（I）请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
（Ⅱ）写出付款金额关于购买量的函数解析式；
（Ⅲ）如果某人付款2100元，求其购买苹果的数量．
【题目】小明与小红开展读书比赛．小明找出了一本以前已读完84页的古典名著打算继续往下读，小红上个周末恰好刚买了同一版本的这本名著，不过还没开始读．于是，两人开始了读书比赛．他们利用下表来记录了两人5天的读书进程．例如，第5天结束时，小明还领先小红24页，此时两人所读到位置的页码之和为424．已知两人各自每天所读页数相同．
读书天数 | 1 | 2 | 3 | 4 | 5 |
页码之差 | 72 | 60 | 48 | 36 | 24 |
页码之和 | 152 | 220 | 424 |
（1）表中空白部分从左到右2个数据依次为 ， ；
（2）小明、小红每人每天各读多少页？
（3）已知这本名著有488页，问：从第6天起，小明至少平均每天要比原来多读几页，才能确保第10天结束时还不被小红超过？（答案取整数）
