题目内容
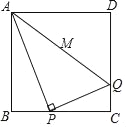
【题目】正方形ABCD的边长为4,P为BC边上的动点,连接AP,作PQ⊥PA交CD边于点Q.当点P从B运动到C时,线段AQ的中点M所经过的路径长( )
A. 2 B. 1 C. 4 D. ![]()
【答案】B
【解析】
分析: 由题意知:PQ⊥AP,即:∠APB+∠QPC=90°,∠BAP+∠APB=180°-∠B=90°,所以∠QPC=∠BAP,又∠B=∠C,即:△ABP∽△PCQ,由相似三角形的性质可得:![]() =
=![]() ,CQ=
,CQ=![]() ×BP,又BP=x,PC=BC-BP=4-x,AB=4,将其代入该式求出CQ的值即可,利用“配方法”求该函数的最大值.易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=
×BP,又BP=x,PC=BC-BP=4-x,AB=4,将其代入该式求出CQ的值即可,利用“配方法”求该函数的最大值.易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=![]() CQ=
CQ=![]() .
.
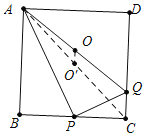
详解: 如图,连接AC,设AC的中点为O′,AQ的中点为O.设BP的长为xcm,CQ的长为ycm.
∵四边形ABCD是正方形,
∴∠B=∠C=90°
∵PQ⊥AP,
∴∠APB+∠QPC=90°
∠APB+∠BAP=90°
∴∠BAP=∠QPC
∴△ABP∽△PCQ
∴![]() =
=![]() ,即
,即![]() ,
,
∴y=-![]() x2+x=-
x2+x=-![]() (x-2)2+1(0<x<4);
(x-2)2+1(0<x<4);
∴当x=2时,y有最大值1cm.
易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=![]() CQ=
CQ=![]() ,
,
∴点O的运动轨迹的路径的长为2OO′=1,
故答案为1.
点睛: 本题主要考查正方形的性质、二次函数的应用、三角形的中位线定理等知识,关键在于理解题意运用三角形的相似性质求出y与x之间的函数关系,学会探究点O的运动轨迹.

练习册系列答案
相关题目