ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψBΘ®aΘ§bΘ©‘ΎΒΎ“ΜœσœόΘ§ΙΐBΉςBAΓΆy÷α”ΎAΘ§ΙΐBΉςBCΓΆx÷α”ΎCΘ§«“ Β ΐaΓΔb¬ζΉψΘ®a-b-2Θ©2+|2a+b-10|Γή0Θ§Κ§45Ϋ«ΒΡRtΓςDEFΒΡ“ΜΧθ÷±Ϋ«±ΏDF”κx÷α÷ΊΚœΘ§DEΓΆx÷α”ΎDΘ§ΒψF”κΉχ±ξ‘≠Βψ÷ΊΚœΘ§DE=DF=3Θ°ΓςDEF¥”Ρ≥ ±ΩΧΩΣ Φ―ΊΉ≈Ήχ±ξ÷α“‘1ΗωΒΞΈΜ≥ΛΕ»ΟΩΟκΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΟκΘ°
Θ®1Θ©«σΒψBΒΡΉχ±ξΘΜ
Θ®2Θ©»τΓςDEF―ΊΉ≈y÷αΗΚΖΫœρ‘ΥΕ·Θ§Ν§Ϋ”AEΘ§EGΤΫΖ÷ΓœAEFΘ§EHΤΫΖ÷ΓœAEDΘ§Β±EGΓΈDF ±Θ§«σΓœHEFΒΡΕ» ΐΘΜ
Θ®3Θ©»τΓςDEF―ΊΉ≈x÷α’ΐΖΫœρ‘ΥΕ·Θ§‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§Φ«ΓςAEF”κ≥ΛΖΫ–ΈOABC÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§Β±0ΘΦtΓή4Θ§S=![]() ±Θ§«κΡψ«σ≥ω‘ΥΕ· ±ΦδtΘ°
±Θ§«κΡψ«σ≥ω‘ΥΕ· ±ΦδtΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©BΘ®4Θ§2Θ©ΘΜΘ®2Θ©ΓœHEF==22.5ΓψΘΜΘ®3Θ©t=1Μρ4s.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”ΟΖ«ΗΚ ΐΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©Β±EGΓΈDF ±Θ§÷Μ“Σ÷ΛΟςΓœAWED=135ΓψΘ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
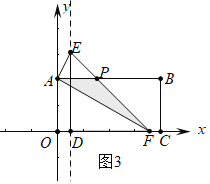
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΔΌ»γΆΦ2÷–Θ§Β±0ΘΦtΘΦ2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςAPFΘ§S=![]() Θ®2-tΘ©t=t-
Θ®2-tΘ©t=t-![]() t2Θ§ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=
t2Θ§ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=![]() Θ®t-2Θ©2=t-2Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®t-2Θ©2=t-2Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©ΓΏΘ®a-b-2Θ©2+|2a+b-10|Γή0Θ§
”÷ΓΏΘ®a-b-2Θ©2Γί0Θ§|2a+b-10|Γί0Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
ΓύBΘ®4Θ§2Θ©Θ°
Θ®2Θ©»γΆΦ1÷–Θ§…ηEGΫΜy÷α”ΎNΘ°
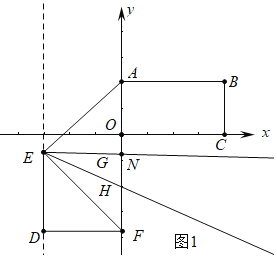
Β±EGΓΈDF ±Θ§ΓœNEF=ΓœEFD=45ΓψΘ§
ΓΏΓœAEF=90ΓψΘ§
ΓύΓœAEN=45ΓψΘ§
ÿDEøFNȧENøDFȧ
ΓύΥΡ±Ώ–ΈDENF «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΓœEDF=90ΓψΘ§DE=DFΘ§
ΓύΥΡ±Ώ–ΈDENF «’ΐΖΫ–ΈΘ§
ΓύΓœDEN=90ΓψΘ§
ΓύΓœAED=135ΓψΘ§
ΓΏEHΤΫΖ÷ΓœAEDΘ§
ΓύΓœDEH=![]() ΓΝ135Γψ=67.5ΓψΘ§
ΓΝ135Γψ=67.5ΓψΘ§
ΓΏΓœDEF=45ΓψΘ§
ΓύΓœHEF=ΓœDEH-ΓœDEF=22.5ΓψΘ°
Θ®3Θ©ΔΌ»γΆΦ2÷–Θ§Β±0ΘΦtΘΦ2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςAPFΘ§S=![]() Θ®2-tΘ©t=t-
Θ®2-tΘ©t=t-![]() t2Θ§
t2Θ§

”…Χβ“βΘΚt-![]() t2=
t2=![]() tȧ
tȧ
ΫβΒΟt=1Θ§Θ°
ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=![]() Θ®t-2Θ©2=t-2Θ§
Θ®t-2Θ©2=t-2Θ§
”…Χβ“βΘΚt-2=![]() tΘ§ΫβΒΟt=4Θ§
tΘ§ΫβΒΟt=4Θ§
Ήέ…œΥυ ωΘ§Β±t=1Μρ4s ±Θ§¬ζΉψΧθΦΰΘ§S=![]() tΘ°
tΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΟϊΕ”‘±≤ΈΦ”…δΜς―ΒΝΖΘ§≥…Φ®Ζ÷±π±Μ÷Τ≥…œ¬Ν–ΝΫΗωΆ≥ΦΤΆΦΘΚ

ΗυΨί“‘…œ–≈œΔΘ§’ϊάμΖ÷Έω ΐΨί»γœ¬ΘΚ
ΤΫΨυ≥…Φ®/ΜΖ | ÷–ΈΜ ΐ/ΜΖ | ÷Ύ ΐ/ΜΖ | ΖΫ≤ν | |
ΦΉ | a | 7 | 7 | 1.2 |
““ | 7 | b | 8 | c |
Θ®1Θ©–¥≥ω±μΗώ÷–aΘ§bΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©Ζ÷±π‘Υ”Ο±μ÷–ΒΡΥΡΗωΆ≥ΦΤΝΩΘ§Φρ“ΣΖ÷Έω’βΝΫΟϊΕ”‘±ΒΡ…δΜς―ΒΝΖ≥…Φ®Θ°»τ―Γ≈…Τδ÷–“ΜΟϊ≤Έ»ϋΘ§Ρψ»œΈΣ”Π―ΓΡΡΟϊΕ”‘±Θ°