Question

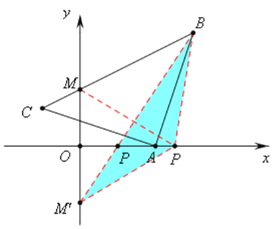
【题目】如图，在平面直角坐标系中，等腰直角三角形的顶点在轴上，，且，交轴于，

（1）求点的坐标；

（2）连接，求的面积；

（3）在轴上有一动点，当的值最小时，求此时的坐标．

Answer 1

【答案】（1）C的坐标是（-1,1）；（2）；（3）P(1,0)

【解析】

（1）作CD⊥x轴于D，BE⊥x轴于E，利用三角形全等的判定定理AAS证明△CDA≌△AEB，即可CD=AE，AD=BE，已知A（2,0）、B（3,3），即可求出C点坐标．

（2）已知B（3,3），C（-1,1）可求出直线BC的解析式，M点坐标，根据各点坐标，S四边形OMBE-S△OMA-S△BEA即可求解．

（3）作M关于x轴的对称点 (0,-1.5)，连接BM’，交x轴于P，此时PB+PM的值最小，

可求得直线B的解析式，即可求出P点坐标．

（1）如图，作CD⊥x轴于D，BE⊥x轴于E，

∵AB=AC，∠BAC=90°

∴∠CAD+∠BAE=90°，

∵作CD⊥x轴于D，

∴∠CAD+∠DCA=90°，

∴∠BAE=∠DCA

∵∠CDA=∠AEB=90°，AC=AB

∴△CDA≌△AEB（AAS），

∴CD=AE，AD=BE

∵A（2,0）、B（3,3），

∴OA=2，OE=BE=3，

∴CD=AE=1，AD=BE=3，

∴OD=AD-OA=1

∴C的坐标是（-1,1）

故答案为：（-1,1）

（2）∵B（3,3），C（-1,1）

设直线BC的解析式为y=kx+b

则

解得

∴直线BC的解析式为

令x=0

y=

∴

∴OM=

∵S四边形OMBE-S△OMA-S△BEA=

故答案为：

（3）如图，作M关于x轴的对称点 (0,-1.5)，连接BM’，交x轴于P，此时PB+PM的值最小，

设直线B的解析式为y=kx+b，得

解得

∴

∵点P在x轴上，

∴当y=0时，x=1

∴P(1,0)