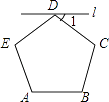题目内容
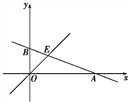
【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把![]() 的值叫做这个菱形的“形变度”;例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
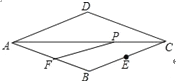
的值叫做这个菱形的“形变度”;例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:![]() ;如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A'E'F',若这个菱形的“形变度”k=
;如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A'E'F',若这个菱形的“形变度”k=![]() ,则
,则![]() _______;
_______;

【答案】![]()
【解析】分析:求出形变前正方形的面积,形变后菱形的面积,两面积之比=菱形的“形变度”,求△AEF的面积,根据两面积之比=菱形的“形变度”,即可解答.
详解:
如图, 在图2中,形变前正方形的面积为:a2,形变后的菱形的面积为:a
在图2中,形变前正方形的面积为:a2,形变后的菱形的面积为:a![]() ,
,
∴菱形形变前的面积与形变后的面积之比:a2:![]() =2:
=2:![]() ,
,
∵这个菱形的“形变度”为2:![]() .
.
∴菱形形变前的面积与形变后的面积之比=这个菱形的“形变度”,
∴S△AEF=![]() ,
,
∵若这个菱形的“形变度”k=![]() ,
,
∴![]() ,
,
又∵S△AEF![]() ,
,
∴![]() .
.
故答案是:![]()

练习册系列答案
相关题目