题目内容
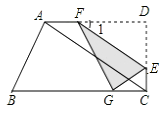
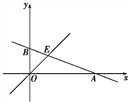
【题目】如图,已知函数y=-![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-![]() x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
【答案】(1)A点的坐标为(12,0);(2)a=6
【解析】分析:(1)根据函数的解析式求出E点的坐标,然后根据待定系数法求出b的值,然后求出与x轴的坐标即可;
(2)根据F点的坐标和垂直的意义,得到C、D点的横坐标均为a,然后根据两点的距离和平行四边形的性质得CD=OB,列方程求解即可.
详解:(1)把x=3代入y=x,得y=3,即E(3,3),
把点E的坐标代入y=-![]() x+b中,得b=4,
x+b中,得b=4,
故函数解析式为y=-![]() x+4,
x+4,
令y=0,得0=-![]() x+4,解得x=12,
x+4,解得x=12,
故A点的坐标为(12,0).
(2)直线AB的解析式为y=-![]() x+4,
x+4,
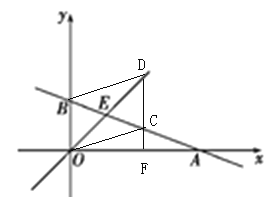
由题意可知,点C、D的横坐标均为a,
∴C![]() ,D(a,a),
,D(a,a),
∴CD=![]() =
=![]() ,
,
∵以点B、O、C、D为顶点的四边形为平行四边形,
∴CD=OB=4,即![]() =4,
=4,
解得a=6或a=0.经验证,当a=0时,直线CD与OB重合,不合题意,当a=6时符合题意.故a=6.

练习册系列答案
相关题目