题目内容
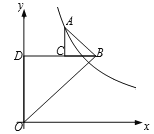
【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,顶点为D. 
(1)求顶点D的坐标.
(2)求△OCD的面积.
【答案】
(1)解:y=﹣x2+2x+3
=﹣(x2﹣2x+1﹣1)+3
=﹣(x﹣1)2+4,
即顶点D的坐标为(1,4)
(2)解:把x=0代入y=﹣x2+2x+3得:y=3,
即OC=3,
所以△OCD的面积为 ![]() 3×1=
3×1= ![]()
【解析】(1)把解析式化成顶点式,即可得出答案;(2)求出OC的长,再根据三角形的面积公式求出即可.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

练习册系列答案
相关题目
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是