题目内容
【题目】已知抛物线C1:y=(x-1)2+1与y轴交于点A,过点A与点(1,3)的直线与C1交于点B
(1) 求直线AB的函数表达式
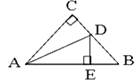
(2) 如图1,若点P为直线AB下方的C1上一点,求点P到直线AB的距离的最大值
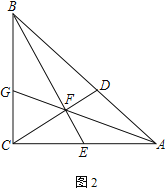
(3) 如图2,将直线AB绕点A顺时针旋转90°后恰好经过C1的顶点C,沿射线AC的方向平移抛物线C1得到抛物线C2,C2的顶点为D,两抛物线相交于点E.设交点E的横坐标为m.若∠AED=90°,求m的值


【答案】(1) y=x+2(2)![]() (3)m=1+
(3)m=1+![]()
【解析】(1) y=x+2
(2) 设P(a,a2-2a+2)
过点P作PQ∥y交轴交AB于Q
∴Q(a,a+2)
∴PQ=(a+2)-(a2-2a+2)=-a2+3a=![]()
当![]() 时,PQ有最大值为
时,PQ有最大值为![]()
过点P作PM⊥AB于M
∵直线AB与竖直方向的夹角为45°
∴△PQM为等腰直角三角形
∴PM=![]()
即P到AB的距离的最大值为![]()
方法2:P在平行于AB且于抛物线相切的切点处
(3) 直线AD的解析式为y=-x+2
设D(n,-n+2)
∴C2:y=(x-n)2-n+2
∵E(m,m2-2m+2)同时也在C2上
∴(m-n)2-n+2=m2-2m+2
整理得:(2m-n)(n-1)=0,n=2m或n=1(舍去)
∴D(2m,-2m+2)
接下来使用K字型
过点E作MN∥x轴交y轴于M,过点D作DN⊥MN于N
∴△DNE∽△EMA
∴DN·AM=ME·EN
即[(m2-2m+2)-(-2m+2)]·[(m2-2m+2)-2]=m2,m2-2m-1=0
解得![]()
∵m>0
∴![]()

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
次数 | 选手甲的成绩(环) | 选手乙的成绩(环) |
1 | 9.6 | 9.5 |
2 | 9.7 | 9.9 |
3 | 10.5 | 10.3 |
4 | 10.0 | 9.7 |
5 | 9.7 | 10.5 |
6 | 9.9 | 10.3 |
7 | 10.0 | 10.0 |
8 | 10.6 | 9.8 |
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?