题目内容
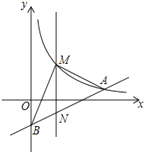
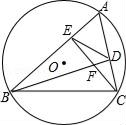
【题目】如图,⊙O的半径为2,弦BC=2![]() ,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
①∠A始终为60°;
②当∠ABC=45°时,AE=EF;
③当△ABC为锐角三角形时,ED=![]() ;
;
④线段ED的垂直平分线必平分弦BC.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
【答案】①②③④
【解析】分析:①延长CO交⊙O于点G,如图1.在Rt△BGC中,运用三角函数就可解决问题;②只需证到△BEF≌△CEA即可;③易证△AEC∽△ADB,则![]() ,从而可证到△AED∽△ACB,则有
,从而可证到△AED∽△ACB,则有![]() .由∠A=60°可得到
.由∠A=60°可得到![]() ,进而可得到ED=
,进而可得到ED=![]() ;④取BC中点H,连接EH、DH,根据直角三角形斜边上的中线等于斜边的一半可得EH=DH=
;④取BC中点H,连接EH、DH,根据直角三角形斜边上的中线等于斜边的一半可得EH=DH=![]() BC,所以线段ED的垂直平分线必平分弦BC.
BC,所以线段ED的垂直平分线必平分弦BC.
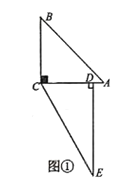
详解:①延长CO交⊙O于点G,如图1.

则有∠BGC=∠BAC.
∵CG为⊙O的直径,∴∠CBG=90°.
∴sin∠BGC=![]() .
.
∴∠BGC=60°.
∴∠BAC=60°.
故①正确.
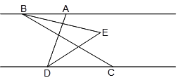
②如图2,

∵∠ABC=45°,CE⊥AB,即∠BEC=90°,
∴∠ECB=45°=∠EBC.
∴EB=EC.
∵CE⊥AB,BD⊥AC,
∴∠BEC=∠BDC=90°.
∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°.
∵∠EFB=∠DFC,∴∠EBF=∠DCF.
在△BEF和△CEA中,
 ,
,
∴△BEF≌△CEA.
∴AE=EF.
故②正确.
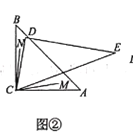
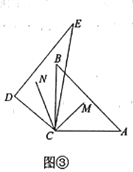
③如图3,
∵∠AEC=∠ADB=90°,∠A=∠A,
∴△AEC∽△ADB.
∴![]() .
.
∵∠A=∠A,
∴△AED∽△ACB.
∴![]() .
.
∵cosA=![]() =cos60°=
=cos60°=![]() ,
,
∴![]() .
.
∴ED=![]() BC=
BC=![]() .
.
故③正确.
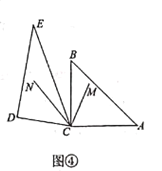
④取BC中点H,连接EH、DH,如图3、图4.
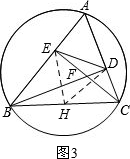

∵∠BEC=∠CDB=90°,点H为BC的中点,
∴EH=DH=![]() BC.
BC.
∴点H在线段DE的垂直平分线上,
即线段ED的垂直平分线平分弦BC.
故④正确.
故答案为:①②③④.