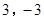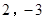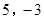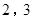��Ŀ����
���Ķ����ϣ���һ��أ�n����ͬ������a��ˣ� ��Ϊ
��Ϊ ����2��2��2=23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊ
����2��2��2=23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊ ����
����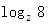 =
= =3������һ��أ���an=b��a>0��a��1��b>0������n������aΪ��b�Ķ�������Ϊ
=3������һ��أ���an=b��a>0��a��1��b>0������n������aΪ��b�Ķ�������Ϊ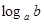 ����
����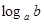 =
= =n������34=81����4������3Ϊ��81�Ķ�������Ϊ
=n������34=81����4������3Ϊ��81�Ķ�������Ϊ ����
���� =
= =4����
=4����
��1���������и�������ֵ��
 4=" _____________________________" ��
4=" _____________________________" �� 16="__________________________" ��
16="__________________________" ��
 64=____________________________��
64=____________________________��
��2���۲죨1�����е�������4��16��64֮����������Ĺ�ϵʽ
 4��
4�� 16��
16�� 64�ִ��������Ĺ�ϵʽ��
64�ִ��������Ĺ�ϵʽ��
��3���ɣ�2������� M+
M+ N=_____________________��a>0��a��1��M>0��N>0����������ݵ����㷨��am•an=am+n����֤����
N=_____________________��a>0��a��1��M>0��N>0����������ݵ����㷨��am•an=am+n����֤����
 ��Ϊ
��Ϊ ����2��2��2=23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊ
����2��2��2=23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊ ����
����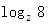 =
= =3������һ��أ���an=b��a>0��a��1��b>0������n������aΪ��b�Ķ�������Ϊ
=3������һ��أ���an=b��a>0��a��1��b>0������n������aΪ��b�Ķ�������Ϊ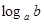 ����
����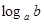 =
= =n������34=81����4������3Ϊ��81�Ķ�������Ϊ
=n������34=81����4������3Ϊ��81�Ķ�������Ϊ ����
���� =
= =4����
=4������1���������и�������ֵ��
 4=" _____________________________" ��
4=" _____________________________" �� 16="__________________________" ��
16="__________________________" �� 64=____________________________��
64=____________________________����2���۲죨1�����е�������4��16��64֮����������Ĺ�ϵʽ
 4��
4�� 16��
16�� 64�ִ��������Ĺ�ϵʽ��
64�ִ��������Ĺ�ϵʽ�� ��3���ɣ�2�������
 M+
M+ N=_____________________��a>0��a��1��M>0��N>0����������ݵ����㷨��am•an=am+n����֤����
N=_____________________��a>0��a��1��M>0��N>0����������ݵ����㷨��am•an=am+n����֤������1��2��4��6����2��4��16=64�� 4+
4+ 16=
16= 64����3���S
64����3���S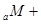 �S
�S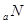 =�S
=�S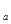 MN��֤�������������
MN��֤�������������
 4+
4+ 16=
16= 64����3���S
64����3���S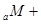 �S
�S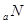 =�S
=�S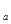 MN��֤�������������
MN��֤�������������������������������Ķ���Ŀ��ȷ��������Ķ��壬���պö�����ָ���Ĺ�ϵ��
��1�����ݶ����Ķ�����⣻��2������۲죬�����ҵ����ɣ�4��16=64��log24+log216=log264����3�������һ�㣬�ó����ۣ�logaM+logaN=loga��MN����֤��ʱ����logaM=b1��logaN=b2���ٸ����ݵ����㷨��an•am=an+m�Լ������ĺ���֤�����ۣ�
�����������1��log24=2��log216=4��log264=6��
��2��4��16=64��log24+log216=log264��
��3��logaM+logaN=loga��MN����֤�����£���logaM=b1��logaN=b2����
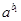 =M��
=M��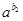 =N������MN=
=N������MN=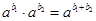 ������b1+b2=loga��MN����logaM+logaN=loga��MN����
������b1+b2=loga��MN����logaM+logaN=loga��MN����
��ϰ��ϵ�д�
�����Ŀ
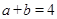 ��
��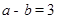 ����
����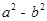 =____________��
=____________��



 ��һ����ȫƽ��ʽ����m��ֵΪ�� ��
��һ����ȫƽ��ʽ����m��ֵΪ�� ��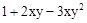 �Ĵ�������ߴ����ϵ���ֱ���
�Ĵ�������ߴ����ϵ���ֱ���