Question

【题目】抛物线y=﹣x2+bx+c（b，c均是常数）经过点O（0，0），A（4，4），与x轴的另一交点为点B，且抛物线对称轴与线段OA交于点P．

（1）求该抛物线的解析式和顶点坐标；

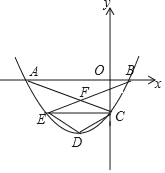
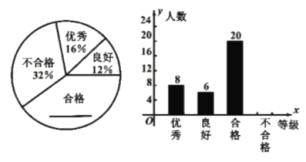
（2）过点P作x轴的平行线l，若点Q是直线上的动点，连接QB．

①若点O关于直线QB的对称点为点C，当点C恰好在直线l上时，求点Q的坐标；

②若点O关于直线QB的对称点为点D，当线段AD的长最短时，求点Q的坐标（直接写出答案即可）．

Answer 1

【答案】（1）y=﹣（x﹣）2+；（，）；（2）①（﹣，）或（，）；②（0，）；

【解析】

1)把0(0,0),A(4,4v3)的坐标代入

y=﹣x2+bx+c,转化为解方程组即可.

(2)先求出直线OA的解析式,点B坐标,抛物线的对称轴即可解决问题.

(3)①如图1中,点O关于直线BQ的对称点为点C,当点C恰好在直线l上时,首先证明四边形BOQC是菱形,设Q（m，）,根据OQ=OB=5,可得方程,解方程即可解决问题.

②如图2中,由题意点D在以B为圆心5为半径的OB上运动,当A,D、B共线时,线段AD最小,设OD与BQ交于点H.先求出D、H两点坐标,再求出直线BH的解析式即可解决问题.

（1）把O（0，0），A（4，4）的坐标代入y=﹣x2+bx+c，

得，

解得，

∴抛物线的解析式为y=﹣x2+5x=﹣（x﹣）2+．

所以抛物线的顶点坐标为（，）；

（2）①由题意B（5，0），A（4，4），

∴直线OA的解析式为y=x，AB==7，

∵抛物线的对称轴x=，

∴P（，）．

如图1中，点O关于直线BQ的对称点为点C，当点C恰好在直线l上时，

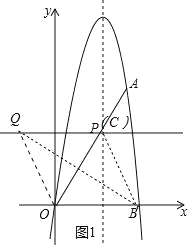
∵QC∥OB，

∴∠CQB=∠QBO=∠QBC，

∴CQ=BC=OB=5，

∴四边形BOQC是平行四边形，

∵BO=BC，

∴四边形BOQC是菱形，

设Q（m，），

∴OQ=OB=5，

∴m2+（）2=52，

∴m=±，

∴点Q坐标为（﹣，）或（，）；

②如图2中，由题意点D在以B为圆心5为半径的⊙B上运动，当A、D、B共线时，线段AD最小，设OD与BQ交于点H．

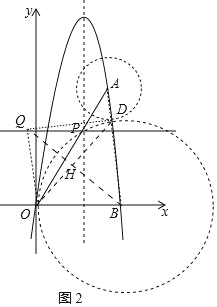
∵AB=7，BD=5，

∴AD=2，D（，），

∵OH=HD，

∴H（，），

∴直线BH的解析式为y=﹣x+，

当y=时，x=0，

∴Q（0，）．