题目内容
【题目】如果两个三角形两边和第三边上的中线对应成比例,那么这两个三角形相似.________(判断对错)
【答案】正确
【解析】
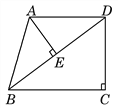
首先根据题意画出图形.已知,AD、A′D′分别是△ABC与△A′B′C′的中线,![]() .再作出辅助线倍长中线法:延长AD到M,使DM=AD,连结MC,证明△ABD≌△MCD,那么AB=MC,同理得出A′B′=M′C′,然后证明△ACM∽△A′C′M′,得出∠MAC=∠M′A′C′,同理可得∠MAB=∠M′A′B′,于是∠BAC=∠B′A′C′,再根据两边及其夹角法即可证明△ABC∽△A′B′C′.
.再作出辅助线倍长中线法:延长AD到M,使DM=AD,连结MC,证明△ABD≌△MCD,那么AB=MC,同理得出A′B′=M′C′,然后证明△ACM∽△A′C′M′,得出∠MAC=∠M′A′C′,同理可得∠MAB=∠M′A′B′,于是∠BAC=∠B′A′C′,再根据两边及其夹角法即可证明△ABC∽△A′B′C′.
正确.理由如下:
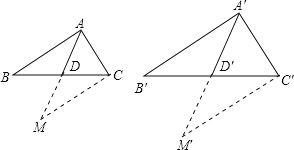
如图,AD、A′D′分别是△ABC与△A′B′C′的中线, ![]()
延长AD到M,使DM=AD,连结MC.
在△ABD与△MCD中,
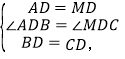
∴△ABD≌△MCD(SAS),
∴AB=MC,
同理延长A′D′到M′,使D′M′=A′D′,连结M′C′,那么A′B′=M′C′,
∴![]()
在△ACM与△A′C′M′中,
![]()
∴△ACM∽△A′C′M′,
∴∠MAC=∠M′A′C′,
同理可得∠MAB=∠M′A′B′,
∴∠MAC+∠MAB=∠M′A′C′+∠M′A′B′,∠BAC=∠B′A′C′.
在△ABC与△A′B′C′中,
![]()
∴△ABC∽△A′B′C′.
故答案为:正确.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目