题目内容
【题目】已知如图,正方形![]() 的边长为4,取
的边长为4,取![]() 边上的中点
边上的中点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ________.
________.
【答案】1
【解析】
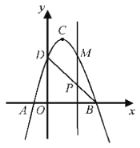
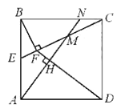
如图,延长DF交AB于P.首先证明EF:CF=1:4,由△ADP≌△BAN,推出BN=AP,DP=AM,由PE∥DC,推出PE:DC=EF:CF=1:4,推出PE=BP=1,再证明∠NCM=∠NMC即可解决问题;
解:如图,延长DF交AB于P.
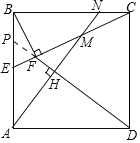
∵四边形ABCD是正方形, ∴AD=AB,∠ABN=∠DAP=90°,
∵AN⊥DP, ∴∠APD+∠PAH=90°,∠ANB+∠PAH=90°,
∴∠APD=∠ANB, ∴△ADP≌△BAN,
∴AN=DP,
∵BF⊥EC, ∴∠EBF+∠BEF=90°,∠BCE+∠BEC=90°,
∴∠EBF=∠BCE, ∴tan∠EBF=tan∠BCE=![]() ,
,
∵AB=BC,BE=AE, ∴tan∠EBF=tan∠BCE= ![]() ,
,
设EF=a,则BF=2a,CF=4a,
∵PE∥DC, ∴![]() ,
,
∵CD=4, ∴PE=1, ∵BE=2, ∴PE=PB=1,
∴PF=![]() BE=1,AP=3,
BE=1,AP=3,
在Rt△ADP中,![]() ,
,
∴DF=4,BN=AP=3,CN=1, ∴BC=DF, ∴∠DFC=∠DCF,
∵∠BCE+∠DCF=90°,∠FMH+∠DFC=90°,∠FMH=∠NMC,
∴∠NCM=∠NMC, ∴MN=CN=1.
故答案为1.

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?