题目内容
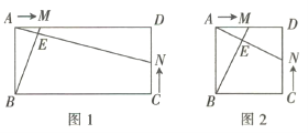
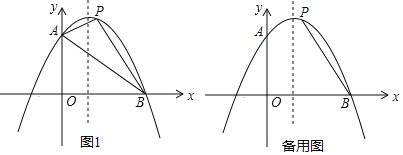
【题目】如图1,已知抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
(1)求这条抛物线的表达式及其顶点坐标;
(2)设点P是抛物线上的动点,若在此抛物线上有且只有三个P点使得△PAB的面积是定值S,求这三个点的坐标及定值S.
(3)若点F是抛物线对称轴上的一点,点P是(2)中位于直线AB上方的点,在抛物线上是否存在一点Q,使得P、Q、B、F为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存请说明理由.
【答案】(1)y=﹣![]() x2+2x+6,顶点坐标为(2,8);(2)点P'(3+3
x2+2x+6,顶点坐标为(2,8);(2)点P'(3+3![]() ,﹣
,﹣![]() ﹣3
﹣3![]() ),P'(3﹣3
),P'(3﹣3![]() ,﹣
,﹣![]() +3
+3![]() ),S=
),S=![]() ;(3)存在,点Q(7,﹣
;(3)存在,点Q(7,﹣![]() )或(﹣1,
)或(﹣1,![]() )或(5,
)或(5,![]() ).
).
【解析】
(1)将交点坐标代入解析式可求解;
(2)设AB上方的抛物线上有点P,过点P作AB的平行线交对称轴于点C,且与抛物线只有一个交点为P,设区PC解析式与抛物线解析式组成方程组,由△=0,可求PC解析式,可求点P坐标,由等底等高的三角形面积相等,可得另两个点所在直线与AB,PC都平行,且与AB的距离等于PC与AB的距离,可求P'E的解析式,即可求解;
(3)分两种情况讨论,由平行四边形的性质可求解.
解:(1)∵抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
∴![]()
∴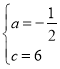
∴抛物线解析式为:y=﹣![]() x2+2x+6,
x2+2x+6,
∵y=﹣![]() x2+2x+6=﹣
x2+2x+6=﹣![]() (x﹣2)2+8,
(x﹣2)2+8,
∴顶点坐标为(2,8)
(2)∵点A(0,6),点B(6,0),
∴直线AB解析式y=﹣x+6,
当x=2时,y=4,
∴点D(2,4)
如图1,设AB上方的抛物线上有点P,过点P作AB的平行线交对称轴于点C,且与抛物线只有一个交点为P,
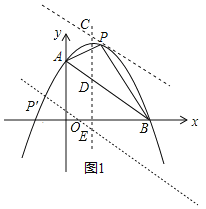
设直线PC解析式为y=﹣x+b,
∴﹣![]() x2+2x+6=﹣x+b,且只有一个交点,
x2+2x+6=﹣x+b,且只有一个交点,
∴△=9﹣4×![]() ×(b﹣6)=0
×(b﹣6)=0
∴b=![]() ,
,
∴直线PC解析式为y=﹣x+![]() ,
,
∴当x=2,y=![]() ,
,
∴点C坐标(2,![]() ),
),
∴CD=![]() ,
,
∵﹣![]() x2+2x+6=﹣x+
x2+2x+6=﹣x+![]() ,
,
∴x=3,
∴点P(3,![]() )
)
∵在此抛物线上有且只有三个P点使得△PAB的面积是定值S,
∴另两个点所在直线与AB,PC都平行,且与AB的距离等于PC与AB的距离,
∴DE=CD=![]() ,
,
∴点E(2,﹣![]() ),
),
设P'E的解析式为y=﹣x+m,
∴﹣![]() =﹣2+m,
=﹣2+m,
∴m=![]()
∴P'E的解析式为y=﹣x+![]() ,
,
∴﹣![]() x2+2x+6=﹣x+
x2+2x+6=﹣x+![]() ,
,
∴x=3±3![]() ,
,
∴点P'(3+3![]() ,﹣
,﹣![]() ﹣3
﹣3![]() ),P'(3﹣3
),P'(3﹣3![]() ,﹣
,﹣![]() +3
+3![]() ),
),
∴S=![]() ×6×(
×6×(![]() ﹣3)=
﹣3)=![]() .
.
(3)设点Q(x,y)
若PB是对角线,
∵P、Q、B、F为顶点的四边形是平行四边形
∴BP与FQ互相平分,
∴![]()
∴x=7
∴点Q(7,﹣![]() );
);
若PB为边,
∵P、Q、B、F为顶点的四边形是平行四边形,
∴BF∥PQ,BF=PQ,或BQ∥FP,BQ=PF,
∴xB﹣xF=xP﹣xQ,或xB﹣xQ=xP﹣xF,
∴xQ=3﹣(6﹣2)=﹣1,或xQ=6﹣(3﹣2)=5,
∴点Q(﹣1,![]() )或(5,
)或(5,![]() );
);
综上所述,点Q(7,﹣![]() )或(﹣1,
)或(﹣1,![]() )或(5,
)或(5,![]() ).
).