题目内容
【题目】奇异果是新西兰的特产,其实它的祖籍在中国,又名“猕猴桃”.2018年1月份至6月份我市某大型超市新西兰品种的奇异果销售价格y(元/盒)与月份x(1≤x≤6,且x为整数)之间的函数关系如下表:

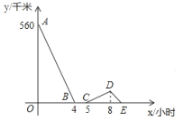
7月份至12月份奇异果的销售价格y(元/盒)与月份x之间满足函数关系式:y=2x+20(7≤x≤12且x为整数).该超市去年奇异果销售数量z(盒)与月份x(1≤x≤12,且x为整数)之间存在如图所示的变化趋势.若去年该超市奇异果的进价为每盒20元,销售奇异果需要一名超市员工,该员工每月固定人工费用为1500元.
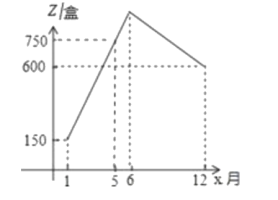
(1)请观察图表中的数据信息直接写出2018年1月份至6月份销售价格y与x之间的函数关系式__ ,根据如图所示的变化趋势,直接写出去年每月销售数量z与x之间满足的函数关系式__ .
(2)求出去年每月该超市的利润w(元)与月份x之间满足的函数关系式.(利润=收入成本费用)
(3)从今年1月份开始,超市决定每卖出一盒奇异果,公司向希望工程捐款2元,奇异果的进价为每盒26元,虽然今年1月份奇异果的销售价格比去年12月份增加4元,但1月份销售数量仍比去年12月份增加了0.4a%;2月份销售价格在1月份的基础上增加了0.5a%,由于其它水果陆续上市,2月份的销售量与1月份持平,这样2月份的利润达到了15780元,请参考以下数据,求出整数a的值.(参考数据:![]() =2025,
=2025,![]() =2116,
=2116,![]() =2209)
=2209)
【答案】(1)y=![]() (1≤x≤6);
(1≤x≤6); 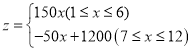 ;(2)
;(2)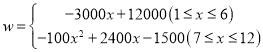 ;(3)
;(3)![]()
【解析】
(1)设2018年1月份至6月份销售价格y与x之间的函数关系式为![]() ,由统计表建立方程组求出其解;设1月份至6月份
,由统计表建立方程组求出其解;设1月份至6月份![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,7月份至12月份
,7月份至12月份![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,根据题意求出结论即可;
,根据题意求出结论即可;
(2)设去年每月该超市的利润w(元),根据利润=收入-成本-费用表示出w就可以求出w与x之间的函数关系式;
(3)根据题意可以求出去年12月的销售价格:y=2×12+20=44元,今年1月份的销售价格为:44+4=48元,去年12月的销售数量为600盒,今年1月份的销售数量为600(1+0.4a%)盒,2月份的销售价格为48(1+0.5a%)元,根据2月份的利润为15780元为等量关系建立方程求出其解即可.
(1)设2018年1月份至6月份销售价格y与x之间的函数关系式为![]() ,由统计表得:
,由统计表得:
![]() ,
,
解得:![]()
∴![]()
![]() (
(![]() );
);
设1月份至6月份![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,由图象,得
,由图象,得
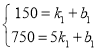 ,
,
解得: ,
,
∴![]() ,(
,(![]() ,
,![]() 为整数)
为整数)
设7月份至12月份![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,由图象,得
,由图象,得
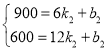 ,
,
解得: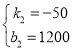
∴![]() (
(![]() ,x为整数),
,x为整数),
∴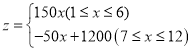 ;
;
(2)设去年每月该超市的利润w(元),由题意,得
当![]() ,x为整数时,
,x为整数时,
![]() =(
=(![]() -20)
-20)![]() ,
,
∴![]()
![]() ;
;
当![]() ,x为整数时,
,x为整数时,
![]()
![]() ,
,
∴![]()
![]() .
.
∴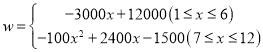 ;
;
(3)由题意,得:
去年12月的销售价格:![]() 元,
元,
今年1月份的销售价格为:44+4=48元,
去年12月的销售数量为:600盒,
今年1月份的销售数量为600(1+0.4a%)盒,
2月份的销售价格为48(1+0.5a%)元,
∴[48(1+0.5a%)-26-2][600(1+0.4a%)]-1500=15780,
设a%=m,则有:
[48(1+0.5m)-26-2][600(1+0.4m)]-1500=15780,
整理,得
12![]()
![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() =
=![]() .
.
∵![]() =2116,
=2116,
∴![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案