题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.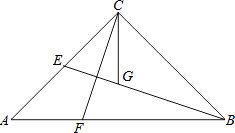
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE.
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵CG平分∠ACB,
∴∠BCG=45°=∠A,
∴∠BCG=∠CAB=45°,
在△ACF和△BCG中,  ,
,
∴△ACF≌△BCG(ASA),
∴AF=CG,CF=BG
(2)解:点G在线段AB的垂直平分线上,如图1所示:理由如下:

∵AC=BC,CG平分∠ACB,
∴CH⊥AB,H为AB中点,
∴点G在线段AB的垂直平分线上
(3)证明:连接AG.如图2所示:

由(2)可知,AG=BG,∠GAB=∠GBA,
∵AD⊥AB,
∴∠GAB+∠GAD=∠GBA+∠D=90°,
∴∠GAD=∠D,
∴GA=GD=GB=CF.
∵AD⊥AB,CH⊥AB
∴CH∥AD,
∴∠D=∠EGC,
∵E为AC中点,
∴AE=EC,
在△AED和△CEG中,  ,
,
∴△AED≌△CEG(SAS),
∴DE=EG,
∴DG=2DE,
∴CF=2DE
【解析】 (1)根据等腰直角三角形的性质及角平分线的定义得出∠BCG=∠CAB=45°,然后由ASA判断出△ACF≌△BCG,然后根据全等三角形的性质得出结论;
(2)根据等腰三角形的三线合一得出CH⊥AB,H为AB中点,故点G在线段AB的垂直平分线上;
(3)连接AG,由垂直的定义得出∠GAD=∠D, 根据等边对等角得出GA=GD=GB=CF,由平行线的判定得出CH∥AD,故∠D=∠EGC,然后由SAS得出△AED≌△CEG,根据全等三角形的性质得出结论。
【考点精析】根据题目的已知条件,利用平行线的判定与性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;等腰三角形的两个底角相等(简称:等边对等角).

 名校课堂系列答案
名校课堂系列答案