题目内容
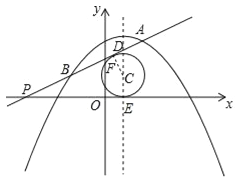
【题目】如图,抛物线y=﹣![]() x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
(1)求抛物线的解析式;
(2)若PA:PB=3:1,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.

【答案】(1) y=﹣![]() x2+
x2+![]() x+3;(2) y=
x+3;(2) y=![]() x+2;(3) 存在,点C的坐标为(1,5
x+2;(3) 存在,点C的坐标为(1,5![]() ﹣10)或(1,﹣5
﹣10)或(1,﹣5![]() ﹣10).
﹣10).
【解析】试题分析: (1)根据抛物线的对称轴为x=1可求出m的值,再将点A的坐标代入抛物线的解析式中求出n值,此题得解;
(2)根据P、A、B三点共线以及PA:PB=3:1结合点A的坐标即可得出点B的纵坐标,将其代入抛物线解析式中即可求出点B的坐标,再根据点A、B的坐标利用待定系数法即可求出直线AP的解析式;
(3)假设存在,设出点C的坐标,依照题意画出图形,根据角的计算找出∠DCF=∠EPF,再通过解直角三角形找出关于r的一元一次方程,解方程求出r值,将其代入点C的坐标中即可得出结论.
试题解析:
解:(1)∵抛物线的对称轴为x=1,
∴﹣![]() =1,解得:m=
=1,解得:m=![]() .
.
将点A(2,3)代入y=﹣![]() x2+
x2+![]() x+n中,
x+n中,
3=﹣1+1+n,解得:n=3,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)∵P、A、B三点共线,PA:PB=3:1,且点A、B位于点P的同侧,
∴yA﹣yP=3yB﹣yP,
又∵点P为x轴上的点,点A(2,3),
∴yB=1.
当y=1时,有﹣![]() x2+
x2+![]() x+3=1,
x+3=1,
解得:x1=﹣2,x2=4(舍去),
∴点B的坐标为(﹣2,1).
将点A(2,3)、B(﹣2,1)代入y=kx+b中,
![]() ,解得:
,解得: 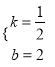 ,
,
∴一次函数的解析式y=![]() x+2.
x+2.
(3)假设存在,设点C的坐标为(1,r).
∵k>0,
∴直线AP的解析式为y=![]() x+2.
x+2.
当y=0时, ![]() x+2=0,
x+2=0,
解得:x=﹣4,
∴点P的坐标为(﹣4,0),
当x=1时,y=![]() ,
,
∴点D的坐标为(1, ![]() ).
).
令⊙与直线AP的切点为F,与x轴的切点为E,抛物线的对称轴与直线AP的交点为D,连接CF,如图所示.
∵∠PFC=∠PEC=90°,∠EPF+∠ECF=∠DCF+∠ECF=180°,
∴∠DCF=∠EPF.
在Rt△CDF中,tan∠DCF=tan∠EPF=![]() ,CD=
,CD=![]() ﹣r,
﹣r,
∴CD=![]() CF=
CF=![]() |r|=
|r|=![]() ﹣r,
﹣r,
解得:r=5![]() ﹣10或r=﹣5
﹣10或r=﹣5![]() ﹣10.
﹣10.
故当k>0时,抛物线的对称轴上存在点C,使得⊙C同时与x轴和直线AP都相切,点C的坐标为(1,5![]() ﹣10)或(1,﹣5
﹣10)或(1,﹣5![]() ﹣10).
﹣10).