题目内容
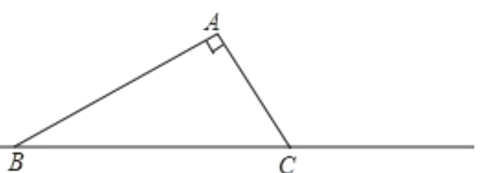
【题目】在平面直角坐标系中,点A(a,0)、B(b,0)(a≠0),a、b满足![]() +b2+2bc+c2=0
+b2+2bc+c2=0
(1) 直接写出a与b的关系
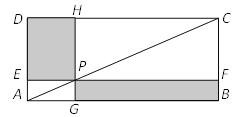
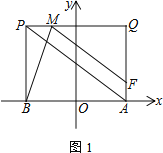
(2) 如图,将线段AB沿y轴的正方向平移m个单位得到线段PQ,点M在线段PQ上,QM=3MP,过M作MF∥PA交QA于点F,连接BM,BM平分∠PMF.若BM=![]() ,求m的值
,求m的值
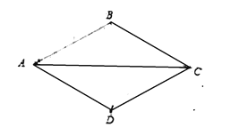
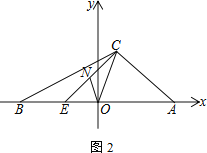
(3) 如图,点C在第一象限内,且满足CA=OA,点E在x轴上,AE=BC,连接CE,取CE的中点N,连接NO.若∠BCA=α,求∠NOC(用含α的代数式表示)
【答案】(1)a+b=0;(2)m=3;(3)∠NOC=90°-0.5ɑ
【解析】
(1)首先由题意,可得出![]() +
+![]() =0,进而可得出
=0,进而可得出![]() ;
;
(2)首先延长MF交x轴于F,得出MP,又因为MF∥PA,PM∥AH,得出四边形PMHA为平行四边形,进而得出AH和BH,又![]() ,即
,即![]() ,再根据BM平分∠PMF,即
,再根据BM平分∠PMF,即![]() ,得出
,得出![]() ,在Rt△PBA中,
,在Rt△PBA中,![]() ,即得出
,即得出
![]() ,即
,即![]() ,
,![]() ,在Rt△PBM中,
,在Rt△PBM中,![]() ,即
,即![]() ,将两个等式联立即可得出
,将两个等式联立即可得出![]() ;
;
(3)首先在OA上取一点F,使得OF=OE,连接CF,由BO=AO,EO=OF,BC=AE,得出BC=BF,进而得出∠BCF=∠BFC,又由N为CE的中点,即EO=OF,得出NO∥CF,进而得出∠NOC=∠OCF,又由∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF,得出∠FCA+∠FAC=∠BCO+∠OCF,又∠COA=∠BCO+∠CBO,将两式联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO,又因为∠FAC+∠CBO=180°-α,得出∠OCF=180°-α-∠COA+∠FCA,又因为∠COA=∠OCF+∠FCA,得出∠OCF=90°-![]() ,即∠NOC=90°-
,即∠NOC=90°-![]() .
.
解:(1)由题意,得
![]() +b2+2bc+c2=0
+b2+2bc+c2=0
![]() +
+![]() =0
=0
∴![]()
∴![]()
(2)延长MF交x轴于F,如图所示
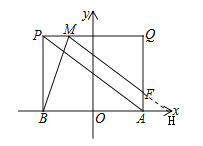
由题意得,P(b,m),Q(a,m)
又∵QM=3MP,
∴![]()
又∵MF∥PA,PM∥AH
∴四边形PMHA为平行四边形
∴![]() ,
,![]()
又![]() ,即
,即![]()
BM平分∠PMF,即![]()
∴![]() ,即
,即![]()
在Rt△PBA中,![]() ,
,![]() ,即
,即![]() ①
①
在Rt△PBM中,![]() ,即
,即
![]() ②
②
联立①②,解得
![]() .
.
(3)在OA上取一点F,使得OF=OE,连接CF,如图所示,
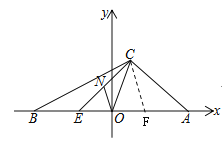
∵BO=AO,EO=OF,BC=AE,
∴BC=BF,
∴∠BCF=∠BFC,
又∵N为CE的中点,即EO=OF
∴NO∥CF
∴∠NOC=∠OCF
又∵∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF
∴∠FCA+∠FAC=∠BCO+∠OCF①
又∠COA=∠BCO+∠CBO②
①②联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO
∵∠FAC+∠CBO=180°-α
∴∠OCF=180°-α-∠COA+∠FCA
又∵∠COA=∠OCF+∠FCA
∴∠OCF=90°-![]()
即∠NOC=90°-![]()