题目内容
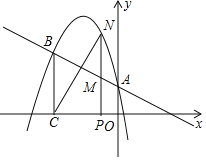
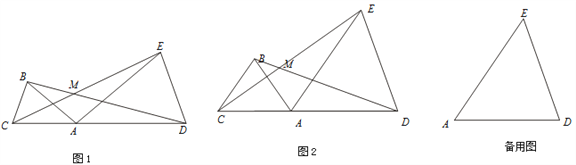
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
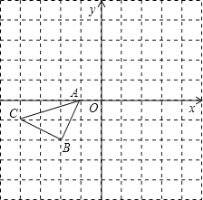
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
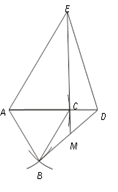
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
【答案】(1)①BD=CE,理由见解析,②180°-2α′;(2)BD=kCE,![]() ;(3)画图见解析,∠BMC=
;(3)画图见解析,∠BMC=![]()
【解析】分析:(1)①先根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC,则∠BAD=∠CAE,再根据SAS证明△ABD≌△ACE,从而得出BD=CE;②先由全等三角形的对应角相等得出∠BDA=∠CEA,再根据三角形的外角性质即可得出∠BMC=∠DAE=180°-2α;(2)先根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC=90°-![]() α,则∠BAD=∠CAE,再由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,则根据两边对应成比例,且夹角相等的两三角形相似证出△ABD∽△ACE,得出BD=kCE,∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=∠DAE=90°-
α,则∠BAD=∠CAE,再由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,则根据两边对应成比例,且夹角相等的两三角形相似证出△ABD∽△ACE,得出BD=kCE,∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=∠DAE=90°-![]() α;(3)先在备用图中利用SSS作出旋转后的图形,再根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC=90°-
α;(3)先在备用图中利用SSS作出旋转后的图形,再根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC=90°-![]() α,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=90°+
α,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=90°+![]() α.
α.
本题解析:(1)①BD=CE,∵AD=AE,∴∠AED=∠ADE=α
∴∠DAE=180°-2∠ADE=180°-2α,同理可得:∠BAC=180°-2α
∴∠DAE =∠BAC∴∠DAE+∠BAE =∠BAC+∠BAE
即:∠BAD =∠CAE
在△ABD与△ACE中
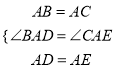 ,
,
∴△ABD≌△ACE(SAS)
∴BD=CE
② ∵△ABD≌△ACE
∴∠BDA =∠CEA
∵∠BMC=∠MCD+∠MDC
∴∠BMC=∠MCD+∠CEA
=∠EAD=180°-2α′
(2)如图2.
∵AD=ED,∠ADE=α,
∴∠DAE= ![]() ,
,
同理可得:∠BAC=90°12α,
∴∠DAE=∠BAC,
∴∠DAE+∠BAE=∠BAC+∠BAE,
即:∠BAD=∠CAE.
∵AB=kAC,AD=kAE,
∴AB:AC=AD:AE=k.
在△ABD与△ACE中,
∵AB:AC=AD:AE=k,∠BDA=∠CEA,
∴△ABD∽△ACE,
∴BD:CE=AB:AC=AD:AE=k,∠BDA=∠CEA,
∴BD=kCE;
∵∠BMC=∠MCD+∠MDC,
∴∠BMC=∠MCD+∠CEA=∠DAE=90°![]() α.
α.
(3)画图:∠BMC= ![]()

【题目】为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?