题目内容
【题目】(为方便答题,可在答题卡上画出你认为必要的图形)
在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰RtRt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
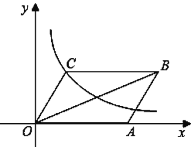
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
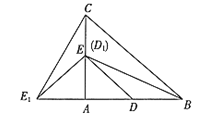
(2)如图2,当α=135°时,求证:BD1=CE1 ,且BD1⊥CE1 ;
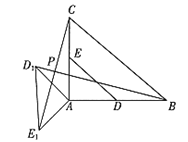
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)
【答案】(1)BD1=![]() ,CE1=
,CE1=![]() ;(2)见解析;(3)1 +
;(2)见解析;(3)1 +![]()
【解析】
(1)结合图1,根据勾股定理可求得BD1、CE1;
(2)根据旋转变换的性质可证明三角形全等,然后由直角三角形的性质可求得结论;
(3)由旋转变换的性质可知,四边形APD1E1为正方形时,距离最大.
解:(1)解:∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
![]() ;
;
(2)证明:当α=135°时,如下图:
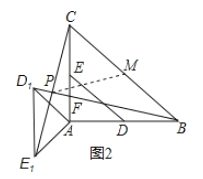
由旋转可知∠D1AB=E1AC=135°
又AB=AC,AD1=AE1,
∴△D1AB ≌ △E1AC
∴BD1=CE1且 ∠D1BA=E1CA
设直线BD1与AC交于点F,有∠BFA=∠CFP
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
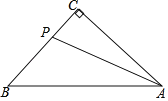
(3)解:如图3,作PG⊥AB,交AB所在直线于点G,
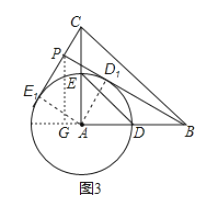
∵D1,E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,则![]() ,
,
故∠ABP=30°,
则![]() ,
,
故点P到AB所在直线的距离的最大值为:![]() .
.

 第1卷单元月考期中期末系列答案
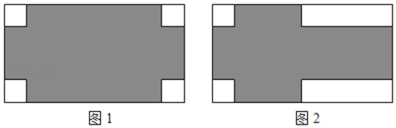
第1卷单元月考期中期末系列答案【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.