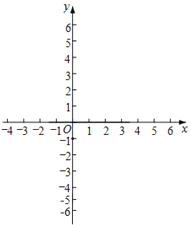题目内容
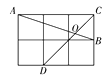
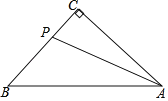
【题目】如图，在等腰Rt△ABC中，∠ACB＝90°，AC＝BC，点P为BC边上一点（不与B、C重合），连接PA，以P为旋转中心，将线段PA顺时针旋转90°，得到线段PD，连接DB．
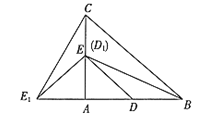
（1）请在图中补全图形；
（2）∠DBA的度数．
【答案】（1）见解析；（2）90°
【解析】
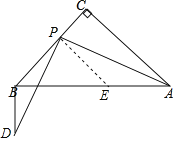
（1）依题意画出图形，如图所示；
（2）先判断出∠BPD＝∠EPA，从而得出△PDB≌△PAE，简单计算即可．
解：（1）依题意补全图形，如图所示，
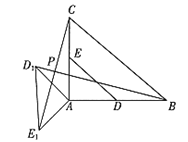
（2）过点P作PE∥AC，
∴∠PEB＝∠CAB，
∵AB＝BC，
∴∠CBA＝∠CAB，
∴∠PEB＝∠PBE，
∴PB＝PE，
∵∠BPD+∠DPE＝∠EPA+∠DPE＝90°，
∴∠BPD＝∠EPA，
∵PA＝PD，
∴△PDB≌△PAE（SAS），
∵∠PBA＝∠PEB＝
（180°﹣90°）＝45°，
∴∠PBD＝∠PEA＝180°﹣∠PEB＝135°，
∴∠DBA＝∠PBD﹣∠PBA＝90°．
状元坊全程突破导练测系列答案【题目】有这样一个问题：探究函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程，请补充完成：
(1)函数y＝(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______；
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m＝_____；
②若M(﹣7，﹣720)，N(n，720)为该函数图象上的两点，则n＝_____；
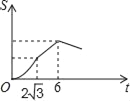
(3)在平面直角坐标系xOy中，A(xA，yA)，B(xB，﹣yA)为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示.
①标出点B的位置；
②画出函数y＝(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y＝
x﹣1与②中你画出图象的交点的横坐标之和为______.
