题目内容
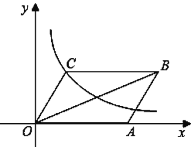
【题目】如图,已如平行四边形OABC中,点O为坐标顶点,点A(3,0),B(4,2),函数![]() (k≠0)的图象经过点C.
(k≠0)的图象经过点C.
(1)求反比例的函数表达式:
(2)请判断平行四边形OABC对角线的交点是否在函数![]() (k≠0)的图象上.
(k≠0)的图象上.
【答案】(1)y=![]() ;(2)平行四边形OABC对角线的交点在函数y=
;(2)平行四边形OABC对角线的交点在函数y=![]() 的图象上,见解析
的图象上,见解析
【解析】
(1)根据平行四边形性质结合点的坐标特征先求得点C的坐标,继而求得答案;
(2)根据平行四边形性质求得对角线交点的坐标,再判断.
(1)∵四边形OABC是平行四边形,A(3,0),
∴CB=OA=3,
又CB∥x轴,B(4,2),
∴C(1,2),
∵点C(1,2)在反比例函数![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=xy=2,
∴反比例的函数表达式y=![]() ;
;
(2)∵四边形OABC是平行四边形,
∴ 对角线的交点即为线段OB的中点,
∵O(0,0),B(4,2),
∴ 对角线的交点为(2,1),
∵2![]() 1=2=k ,
1=2=k ,
∴平行四边形OABC对角线的交点在函数y=![]() 的图象上.
的图象上.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.