题目内容
【题目】已知![]() ,点
,点![]() 为平面内一点,连接
为平面内一点,连接![]() .
.
(1)探究:
如图1:![]() ,
,![]() ,则
,则![]() 的度数是___________;
的度数是___________;
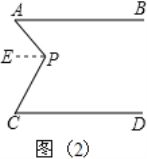
如图2:![]() ,
,![]() ,则
,则![]() 的度数是___________.
的度数是___________.
(2)在图2中试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)拓展探究:当点![]() 在直线
在直线![]() ,
,![]() 外,如图3、4所示的位置时,请分别直接写出
外,如图3、4所示的位置时,请分别直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.

【答案】(1)![]() ;
;![]() .(2)
.(2)![]() 理由见解析;(3)图3.
理由见解析;(3)图3.![]() ,图4.
,图4.![]() .
.
【解析】
(1)①过点P作PQ∥AB,再根据两直线平行,同旁内角互补进行求解;
②过点![]() 作
作![]() ,根据两直线平行,内错角相等进行求解;
,根据两直线平行,内错角相等进行求解;
(2)过点![]() 作
作![]() ,方法同②,把角度换成字母即可求解证明;
,方法同②,把角度换成字母即可求解证明;
(3)根据平行线的性质及三角形的外角定理即可求解.
解:(1)①过点P作PQ∥AB,则PQ∥AB∥CD,
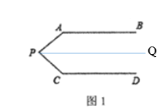
∵![]() ,
,![]() ,
,
∴∠APQ=180°-![]() =35°,
=35°,
∠CPQ=180°-![]() =45°,
=45°,
∴∠APC=∠APQ+∠CPQ=80°
②过点![]() 作
作![]() ,则PE∥AB∥CD,
,则PE∥AB∥CD,
∵![]() ,
,![]() ,
,
∴∠APE=![]() ,∠CPE=
,∠CPE=![]() ,
,
∴![]() =105°
=105°
(2)![]() .
.
理由:如图2.,过点![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;

3.图3:∵AB∥CD
∴∠![]() =∠PEB-∠PAB=
=∠PEB-∠PAB=![]()
即![]() ,
,
图4. ∵AB∥CD
∴∠![]() =∠PFD-∠PCD=
=∠PFD-∠PCD=![]()
即![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?